Шлицев или шлицов как правильно: Склонение слова Шлиц по падежам в единственном и множественном числе

типы, размеры, маркировки – [ СТАТЬЯ ]

Обновлена: 10 Октября 2022
210
0

Поделиться с друзьями

Содержание статьи

  • Типы шлицов отверток

  • Несколько советов


Отвертка является незаменимым ручным инструментом, который предназначается для откручивания и закручивания широкого спектра крепежных элементов с резьбой, а также для наладки или настройки разнообразных электрических приспособлений.


Чтобы понять, что такое шлиц отвертки, необходимо ознакомиться с основными частями инструмента. Как правило, отвертка состоит из трех частей:

  • резиновая, пластиковая или деревянная рукоятка;

  • стальной стержень;

  • рабочая часть (наконечник), который и называется шлицом.


Поскольку наконечник больше других основных частей подвержен механическим воздействиям, изготавливается такая деталь из молибденовых или хромованадиевых сталей. Неправильный выбор шлица отвертки может привести к порче крепежа, что затруднит доступ к устройству или монтажу конструкции. Именно поэтому важно разбираться в разновидностях наконечников. Маркировка помогает разобраться в предлагаемом ассортименте.

Типы шлицов отверток


Самой распространенной является отвертка с прямым шлицем (SL), использующаяся для фиксации шурупов и саморезов в случаях, когда сильное затягивание крепежного элемента не требуется. Работать с таким шлицем неудобно, поскольку жало отвертки периодически соскальзывает или смещается в сторону, что способствует появлению царапин.


Согласно ГОСТ плоские шлицы могут затачиваться под радиусную или классическую форму. Радиусная заточка повышает производительность во время закручивания, но заметно хуже справляется с выполнением нестандартных задач (отгибание или расклинивание деталей).


Крестообразные шлицы образуют группу из нескольких разновидностей:

  • Филлипс (PH) – такая форма самоцентрируется и решает проблему соскальзывания во время закручивания, но в работе с электроинструментами есть риск срыва резьбы или шлица;

  • Позидрайв (PZ) – модернизированная версия PH, которая отличается устойчивым сцеплением и возможностью приложить на инструмент большее крутящее усилие;

  • Фриасон (Freason) – благодаря большим лопастям и четкому углу сведения появляется возможность передавать на биту увеличенный крутящий момент;

  • Супадрив (Supadriv) – разновидность PZ, которая имеет более широкий центр, допускающий осевое смещение наконечника;

  • Phillips II – второе поколение крестообразного шлица PH, которое имеет специальные насечки, повышающие силу сцепления и снижающие выталкивающий эффект;

  • Французский шлиц – двухступенчатая конструкция, отличающаяся увеличивающимся диаметром жала;

  • JIS B 1012 – японская разновидность, отличающаяся сильным скосом, что способствует снижению выталкивания отвертки;

  • Mortorq (оригинальная разработка The Phillips Screw Company) – Поскольку вероятность срыва такого шлица минимальна, активно используется в автомобилестроении и авиационно-космической промышленности.


Основное отличие квадратных шлицев заключается в большом количестве опорных точек, способствующих передаче крутящего момента. Данная группа включает в себя несколько разновидностей:

  • Шлиц Робертсона (Scrulox) – квадрат правильной формы позволяет завинчивать и отвинчивать крепеж одной рукой.

  • LOX-Recess – форма двух смещенных и пересекающихся квадратов образует 12 точек соприкосновения, что уменьшает износ и обеспечивает крепкий контакт.

  • Двойной квадрат – два пересекающихся квадрата без смещения образуют 8-конечную звезду.

  • Тройной квадрат (XZN) – отвертки с наконечником, имеющим форму трех квадратов Робертсона на единой оси, активно используются в автомобилестроении, поскольку обеспечивают большой крутящий момент.


Биты под внутренний шестигранник, как правило, представлены тремя вариациями. Шестигранный шлиц (Аллен, HEX) широко используется в различных областях. Антивандальное исполнение отличается наличием штифта в середине. Двойной шестигранник похож на тройной квадрат XZN, но несовместим с такими элементами крепежа. Шлиц Outlaw имеет ступенчатый сход, что позволяет работать одной отверткой с крепежом любых размеров.


Пятилучевые отвертки, которые обеспечивают хорошее затягивание крепежа, представлены двумя видами. Специалисты компании Apple разработали шлиц Pentalobe, который усложняет несанкционированный разбор дорогостоящих устройств. Пятилучевая бита ASTER recess представляет собой пятиугольник со сферическими выступами на конце. Активно применяется при производстве авиационно-космической техники, когда необходима односторонняя затяжка.


Звездообразные шлицы очень популярны, поскольку не соскальзывают, способны функционировать на очень высокой скорости, а также имеют отличное сцепление с поверхностью крепежных элементов.


Различают 3 основных вида:

  • Torx (бита-звездочка) – выполнен в форме симметричной 6-лучевой звезды, что способствует равномерному воздействию на изделие в момент затяжки;

  • Torx Plus – модернизированный звездообразный шлиц, отличающийся увеличенным основанием и укороченными лучами;

  • Torx ttap – отвертка имеет на конце небольшой штифт, который совпадает с углублением в головке крепежа, что позволяет исключить перекосы при работе инструментом.


Практичные комбинированные шлицы активно используются при производстве электронных изделий и мебельной фурнитуры. Примечательно, что работать с крепежными изделиями, имеющими такой шлиц, можно разными типами отверток, в зависимости от того, какие типы шлицев были взяты за основу. Многие производители выпускают комбинированные отвертки с переставным жалом. Примеры: Филлипс/Квадрат, Clutch (тип A и тип G), SL/Торкс.


Наружные шлицы отверток представляют собой противоположный форм-фактор. То есть, наконечник инструмента имеет углубление определенной формы. Такой крепеж обладает рядом преимуществ: прорези не забиваются грязью или краской, в углублениях не скапливается вода, возможность работы в узких местах, большой выбор инструментов для работы с некоторыми типами шлицев (отвертки, накидные, рожковые и разводные ключи).


Виды шлицев отверток данного типа:

  • квадрат;

  • шестигранник;

  • прямоугольник;

  • наружный Torx;

  • двенадцатигранник.


Антивандальные шлицы представлены большой группой изделий с пазами и выступами сложных форм. Такие изделия выполняют 2 задачи: препятствуют несанкционированному доступу к устройствам, а также мешают снять различные предметы в общественных местах (урны, таблички, пепельницы, указатели и многое другое). Некоторые разновидности антивандальных бит: Bristol, Line, One-way, ALR и DTC, Овал и Треугольник, Polydrive, Спаннер (Snake-Eyes), Torq-set, а также Tri-point, Tri-groove и Tri-Wing.

Несколько советов


Если для работы с определенными видами шлицев на винтах используется специальная отвертка, то никаких затруднений с завинчиванием или отвинчиванием крепежа не возникнет. В случае работы с креплением, подверженным ржавлению, рекомендуется использовать специальные растворители. Нельзя допускать перекоса стержня отвертки по отношению к оси шурупа или иного крепления.


Важно обращать внимание на маркировку отверток. Многие производители предлагают целые наборы с множеством съемных наконечников, что упрощает работу с разными изделиями. Работая с электроникой или деталями, которые могут находиться под напряжением, необходимо использовать диэлектрические инструменты. Также следует соблюдать температурный диапазон работы, который, как правило, варьируется от -40 до +70 градусов по Цельсию.


Была ли статья полезна?

Да

Нет

Оцените статью

Что вам не понравилось?

Другие материалы по теме

Анатолий Мельник

Специалист в области радиоэлектроники и электронных компонентов. Консультант по подбору деталей в компании РадиоЭлемент.

Особенности шлицов саморезов, шурупов и винтов — Висма-Строй

Саморезы и винты – на сегодня производители крепежа выпускают сотни разновидностей.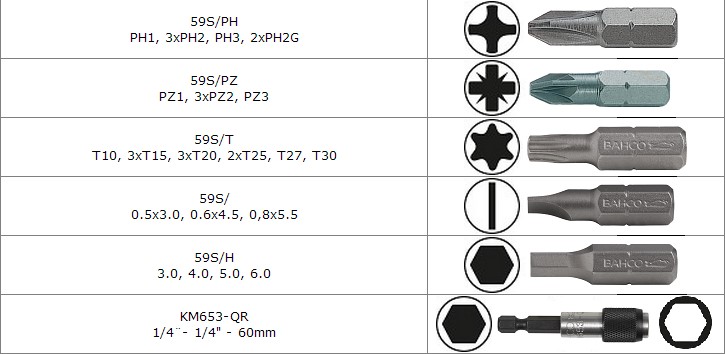 В маркировке запросто можно запутаться — метрическая, дюймовая, с определением шага резьбы, качество стали… В этом разделе мы поговорим типе шлица для саморезов, винтов и шурупов, который является обязательной частью маркировки.

Крепеж с прямым шлицем

Крепеж с прямым шлицем — самый старый на сегодня образец. Прямой шлиц все еще можно найти на старых шурупах и саморезах, однако современные производители планомерно сокращают производство крепежа сданным типом шлица.

Шлицы Филипс

Шлиц крестообразный Phillips – стандарт, внедренный в массовое производство в первой половине 20-го века. Он до сих пор встречается довольно часто, а биты для шуруповерта под этот шлиц по-прежнему востребованы. Однако способность шлица сохранять форму при усиленном демонтаже оказывается ниже новых аналогов- Pozydryv и Frearson. Маркировка биты – PH. В настоящее время стандарт заменяют на Phillips II (Ph3), где шлиц и биты изготовлены со специальными насечками для более прочной фиксации. Ph3 чаще всего используется на мелкихз саморезах («клопы» и проч.)

Шлицы Фрирсон

Шлиц крестообразный Фрирсон (Frearson) – аналог Phillips. Основные отличия – у шлица Frearson прямые углы, у Phillips — закругленные. Удобство Фрирсона заключается в том, что одна бита данного стандарта подходит под любой размер головок с соответствующим шлицом. Использовать Frearson важно с битами своего стандарта. В настоящее время используется достаточно редко.

Шлицы Позидрив

Шлиц крестообразный Позидрив (Pozydryv) – патент на данный тип принадлежит производителю Phillips Screw Company, который придумал и Phillips. Отличительная особенность шлица -дополнительные насечки по углам «креста». В случае с Pozydryv фиксация биты в шлице самореза оказывается лучше Филлипса. Однако важно обращать внимание на маркировку. Для Pozydryv подходит PZ-PZ2. Если при монтаже использовать PH, гарантирован ускоренный износ шляпки крепежного изделия.

Шлицы шестигранные Аллен

Шестигранный шлиц Hex (Allen)- изобретенный еще на заре 20 века (патент выдан в 1910 году), этот тип шлица получил массовое распространение относительно недавно. Мебельные стяжки, конфирматы, велосипедные винты – здесь Hex встречается особенно часто. Для работы с данным типом требуется специальный инструмент – г-образный шестигранный ключ или же шестигранная бита. Среди фигурных невыталкиваемых соединений считается наиболее склонным к срывам с биты. Дополнительный плюс – возможность монтажа под углом (шарообразный инбус).

Шлицы квадратные Робертсон

Квадратный шлиц Робертсона (Scrulox) – считается одним из самых удобных среди современных типов крепежа. Шлиц Робертсона наибольшее распространение получил в Канаде. Здесь его часто используют при изготовлении мебели. Все чаще Робертсон можно встретить в строительстве. Удобство шлица — плотная фиксация биты, которая позволяет работать без соскока даже при вибрационных нагрузках. Крепеж с таким шлицем надежно держится на отвертке.

Шлицы «звездочка»

Шлиц «звездочка» (Torx) – многие специалисты считают это соединение самым надежным на срыв на современном рынке. Крепеж Torx используется преимущественно в автопроме. Имеет антивандальные разновидности Torx Tamper Resistant, 5-lobe Torx (пятиконечный торкс), Torx Plus, где в углублении крепежа располагается специальный штырек.

Шлицы «комби»

Шлиц «комби»- вариант прямого шлица, который может изготавливатьсяв различных вариантах для использования с битами Филипс, Робертсон, Торкс и другими.

Введение в шлицы2

Введение в шлицы2

Вэньцзе Ван
13.01.2023

Пакет R splines2 предназначен для
комплексное, эффективное дополнение к базовому пакету
сплайнов . Он предоставляет функции, создающие различные
базисных функций регрессионного сплайна, которые недоступны из
сплайнов . Большинство функций имеют очень похожий пользователь
интерфейс с функцией splines::bs() . Чтобы быть более
конкретно, он предоставляет функции для построения базисных матриц из

  • B-шлицы
  • M-шлицы
  • I-шлицы
  • С-образные шлицы
  • периодические М-сплайны
  • натуральные кубические сплайны
  • обобщенные многочлены Бернштейна

вместе с их интегралами (кроме C-сплайнов) и производными от
заданный порядок рекурсивными формулами в замкнутой форме.

По сравнению с пакетом сплайнов пакет
splines2 позволяет использовать кусочно-постоянные базисные функции для
B-шлицы и обеспечивает более удобный интерфейс для их
производные с последовательной обработкой на Н/Д с. Большинство из
реализации были (пере)писаны на C++ с помощью
Rcpp и RcppArmadillo начиная с версии 0.3.0,
что повысило вычислительную производительность.

В оставшейся части этой виньетки мы проиллюстрировали основное использование
большинство функций в пакете через примеры. См. руководство по упаковке
для получения подробной информации об использовании функции.

B-сплайны с их интегралами и производными

Функция bSpline() предоставляет базовую матрицу B-сплайна и
позволяет степень = 0 для кусочно-постоянной базисной функции,
который расширяет функцию bs() в пакете
сплайнов с лучшей вычислительной производительностью. Один
пример линейных B-сплайнов с тремя внутренними узлами дан как
следует:

 библиотека (splines2)
узлы <- c(0,3, 0,5, 0,6)
х <- последовательность (0, 1, 0,01)
bsMat <- bSpline(x, узлы = узлы, степень = 1, перехват = ИСТИНА)
matplot(x, bsMat, тип = "l", ylab = "y")
abline(v = узлы, lty = 2, col = "серый")

B-шлицы первой степени с тремя внутренними узлами
0,3, 0,5 и 0,6.

Замкнутая рекуррентная формула интегралов B-сплайна и
производные, данные Де Буром (1978), являются
реализовано в функции ibs() и dbs() ,
соответственно. Ниже приведены два игрушечных примера:

 ibsMat <- ibs(x, узлы = узлы, степень = 1, перехват = ИСТИНА)
пар (mfrow = c (1, 2))
matplot(x, bsMat, тип = "l", ylab = "y")
abline (v = узлы, h = 1, lty = 2, col = "серый")
matplot(x, ibsMat, тип = "l", ylab = "y")
abline(v = узлы, h = c(0,15, 0,2, 0,25), lty = 2, col = "серый")

Кусочно-линейные B-сплайны (слева) и их интегралы
(верно).

 bsMat <- bSpline(x, узлы = узлы, пересечение = ИСТИНА)
dbsMat <- dbs(x, узлы = узлы, перехват = ИСТИНА)
пар (mfrow = c (1, 2))
matplot(x, bsMat, тип = "l", ylab = "y")
abline (v = узлы, lty = 2, col = "серый")
matplot(x, dbsMat, type = "l", ylab = "y")
abline(v = узлы, lty = 2, col = "серый")

Кубический B-сплайн (слева) и их первая производная
(верно).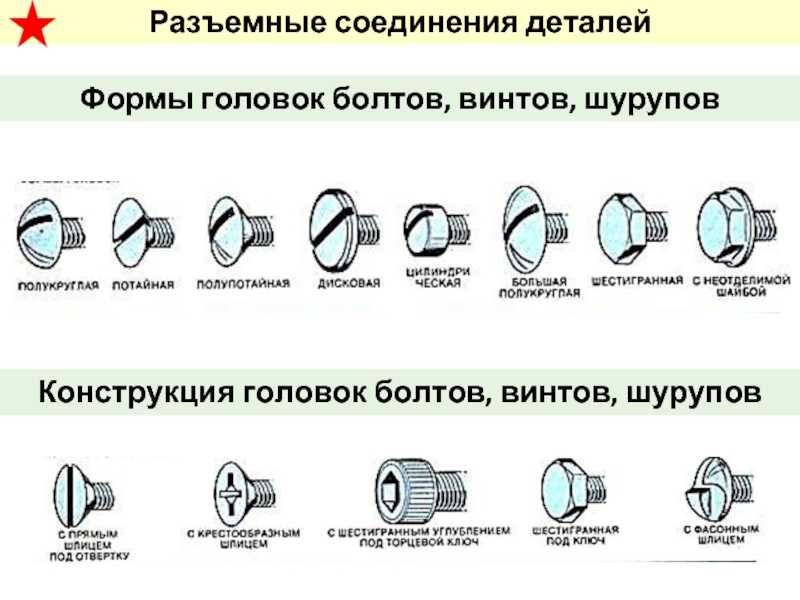

Мы также можем легко получить производные с помощью производное()
следующим образом:

 is_equivalent <- function(a, b) {
    all.equal(a, b, check.attributes = FALSE)
}
stopifnot(is_equivalent(dbsMat, deriv(bsMat)))

M-сплайнов с использованием

mSpline()

M-сплайнов (Ramsay 1988) учитываются
нормализованная версия B-сплайнов с единичным интегралом в пределах границы
узлы. Пример, приведенный Рамзи (1988).
представлял собой квадратичные М-сплайны с тремя внутренними узлами, расположенными на 0,3, 0,5,
и 0,6. Граничные узлы по умолчанию находятся в диапазоне х и
таким образом, 0 и 1 в этом примере.

 msMat <- mSpline(x, узлы = узлы, степень = 2, пересечение = ИСТИНА)
matplot(x, msMat, тип = "l", ylab = "y")
abline(v = узлы, lty = 2, col = "серый")

Квадратичный М-сплайн с тремя внутренними узлами
на 0,3, 0,5 и 0,6.

Производная данного порядка М-сплайнов может быть получена с помощью
указание положительного целого числа в аргументе dervis of
mSpline() . Кроме того, для существующего mSpline
объект, сгенерированный mSpline() , deriv()
метод можно использовать удобно. Например, первая производная от
М-сплайны, приведенные в предыдущем примере, могут быть получены эквивалентно
следующим образом:

 dmsMat1 <- mSpline(x, узлы = узлы, степень = 2, пересечение = ИСТИНА, производные = 1)
dmsMat2 <- производное (msMat)
stopifnot(is_equivalent(dmsMat1, dmsMat2))

Периодические М-сплайны

Функция mSpline() создает периодические сплайны на основе
на основе М-сплайнов, когда периодический = ИСТИНА есть
указано. Boundary.knots определяет циклический интервал.
Конструкция следует периодическим B-сплайнам, обсуждаемым в Piegl and Tiller (1997, глава 12).

 x1 <- seq.int(0, 3, 0,01)
pmsMat <- mSpline(x1, узлы = узлы, степень = 3, перехват = ИСТИНА,
                  периодический = ИСТИНА, Boundary.knots = c(0, 1))
matplot(x1, pmsMat, type = "l", xlab = "x", ylab = "Периодическая основа")
abline(v = seq. int(0, 3), lty = 2, col = "grey")

Кубические периодические М-сплайны.

Мы все еще можем указать аргумент производных в
mSpline() или используйте соответствующий deriv()
метод получения производных, когда периодический = TRUE .

 dpmsMat <- производное(pmsMat)
matplot(x1, dpmsMat, type = "l", xlab = "x", ylab = "1-я производная")
abline(v = seq.int(0, 3), lty = 2, col = "grey")

Первые производные периодических М-сплайнов.

Кроме того, мы можем получить интегралы периодических М-сплайнов по формуле
указание интеграл = ИСТИНА . Интеграл интегрируется из
левый пограничный узел.

 ipmsMat <- mSpline(x1, узлы = узлы, степень = 3, пересечение = ИСТИНА,
                   периодический = ИСТИНА, Boundary.knots = c(0, 1), интеграл = ИСТИНА)
matplot(x1, ipmsMat, type = "l", xlab = "x", ylab = "Интегралы")
abline(v = seq.int(0, 3), h = seq.int(0, 3), lty = 2, col = "gray")

Интегралы периодических М-сплайнов.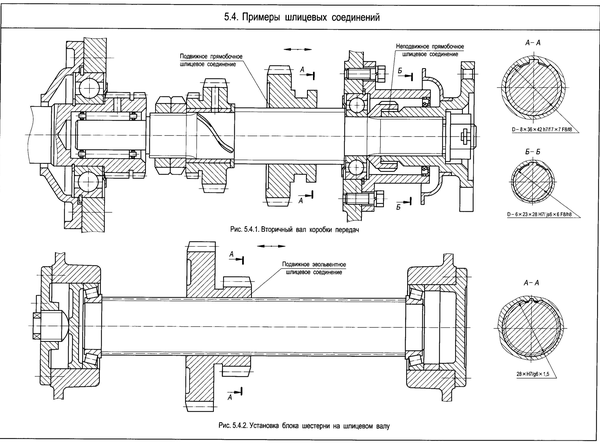

I-сплайнов с использованием

iSpline()

I-сплайнов (Ramsay 1988) просто
интеграл M-сплайнов и, таким образом, монотонно неубывающий с единицей
максимальное значение. Монотонно неубывающая (невозрастающая) функция
может быть оснащена линейной комбинацией базисных функций I-сплайна с
неотрицательные (неположительные) коэффициенты плюс константа , где
коэффициент при константе не ограничен.

Пример, приведенный Ramsay (1988), был
I-сплайны, соответствующие этим квадратичным M-сплайнам с тремя
внутренние узлы размещены на 0,3, 0,5 и 0,6. Обратите внимание, что степень
I-сплайны определяются из связанных M-сплайнов вместо их
полиномиальная степень.

 isMat <- iSpline(x, узлы = узлы, степень = 2, пересечение = ИСТИНА)
matplot (x, isMat, тип = "l", ylab = "y")
abline(h = 1, v = узлы, lty = 2, col = "серый")

I-сплайны второй степени с тремя внутренними узлами
0,3, 0,5 и 0,6.

Соответствующая базисная матрица M-сплайна может быть легко получена как
первые производные I-сплайнов по deriv()
метод.

 stopifnot(is_equivalent(msMat, deriv(isMat)))

Мы можем указать производных = 2 в
deriv() метод вторых производных I-сплайнов,
которые эквивалентны первым производным соответствующих
М-сплайны.

 dmsMat3 <- производное(isMat, 2)
stopifnot (is_equivalent (dmsMat1, dmsMat3))

C-сплайнов с использованием

cSpline

Выпуклых сплайнов (Meyer 2008), называемых
C-сплайны представляют собой масштабированные интегралы I-сплайнов с единичным максимальным значением при
правый пограничный узел. Мейер (2008)
применил C-сплайны к регрессионному анализу с ограничением по форме. монотонность
(неубывающее) свойство I-сплайнов обеспечивает выпуклость C-сплайнов.
Функцию выпуклой регрессии можно оценить с помощью линейных комбинаций
базисных функций C-сплайна с неотрицательными коэффициентами, плюс
неограниченная линейная комбинация константы и тождественной функции
\(г(х)=х\). Если в основе
функция регрессии является одновременно возрастающей и выпуклой, коэффициент при
функция тождества также ограничена неотрицательностью.

Мы можем указать аргумент масштаб = ЛОЖЬ в функции
cSpline() для отключения масштабирования интегралов
I-сплайны. Тогда действительные интегралы соответствующих I-сплайнов будут
быть возвращены. Если масштаб = TRUE (по умолчанию), каждый C-сплайн
базис масштабируется, чтобы иметь единичную высоту в правом граничном узле.

 csMat1 <- cSpline(x, узлы = узлы, степень = 2, пересечение = ИСТИНА)
matplot(x, csMat1, тип = "l", ylab = "y")
abline(h = 1, v = узлы, lty = 2, col = "серый")

С-образные шлицы второй степени с тремя внутренними узлами
0,3, 0,5 и 0,6.

Точно так же метод deriv() можно использовать для получения
производные. Вложенный вызов deriv() поддерживается для
производные порядка больше единицы. Тем не менее, аргумент
производных метода deriv() можно указать
непосредственно для лучшей вычислительной производительности. Например, первый
и вторые производные могут быть получены следующим эквивалентом
подходит соответственно. {n-i},~i\in\{0,\ldots,n\},
\] где \(a\le x\le b\).
Очевидно, оно сводится к регулярным полиномам Бернштейна, определенным над
\([0, 1]\), когда \(a = 0\) и \(b =
1\).

Мы можем получить базисную матрицу обобщения, используя функцию
bernsteinPoly() . Например, многочлены Бернштейна
степени 4 над \([0, 1]\) и является
генерируется следующим образом:

 x1 <- seq.int(0, 1, 0,01)
x2 <- seq.int(- 1, 1, 0,01)
bpMat1 <- bernsteinPoly(x1, степень = 4, перехват = ИСТИНА)
bpMat2 <- bernsteinPoly(x2, степень = 4, перехват = ИСТИНА)
пар (mfrow = c (1, 2))
матплот (x1, bpMat1, тип = "l", ylab = "y")
matplot(x2, bpMat2, type = "l", ylab = "y")

Многочлены Бернштейна степени 4 над [0, 1] (слева)
и обобщенная версия над [- 1, 1] (справа).

Кроме того, мы можем указать интеграл = ИСТИНА или
производных = 1 в bernsteinPoly() для их
интегралы или первые производные соответственно.

 ibpMat1 <- bernsteinPoly(x1, степень = 4, точка пересечения = ИСТИНА, интеграл = ИСТИНА)
ibpMat2 <- bernsteinPoly(x2, степень = 4, точка пересечения = ИСТИНА, интеграл = ИСТИНА)
dbpMat1 <- bernsteinPoly(x1, степень = 4, перехват = ИСТИНА, производные = 1)
dbpMat2 <- bernsteinPoly(x2, степень = 4, перехват = ИСТИНА, производные = 1)
пар (mfrow = c (2, 2))
matplot (x1, ibpMat1, type = "l", ylab = "Интегралы")
matplot (x2, ibpMat2, тип = "l", ylab = "y")
matplot (x1, dbpMat1, тип = "l", ylab = "y")
matplot(x2, dbpMat2, тип = "l", ylab = "y")

Интегралы (верхняя панель) и первые производные
(нижняя панель) полиномов Бернштейна степени 4.

Точно так же мы можем использовать метод deriv() для получения
производные от существующего объекта bernsteinPoly .

 stopifnot(is_equivalent(dbpMat1, deriv(bpMat1)))
stopifnot(is_equivalent(dbpMat2, производная(bpMat2)))
stopifnot(is_equivalent(dbpMat1, производная(ibpMat1, 2)))
stopifnot(is_equivalent(dbpMat2, производная(ibpMat2, 2)))

Натуральные кубические сплайны

Функция naturalSpline() возвращает неотрицательный базис
функции (в пределах границы) для натуральных кубических сплайнов, используя
нулевое пространство закрытой формы, полученное из вторых производных кубического
B-сплайны. В то время как splines::ns() использует декомпозицию QR для
найти нулевое пространство вторых производных базиса B-сплайна в
граничные узлы без гарантии того, что результирующие базисные функции
неотрицательна в пределах границы. Когда интеграл = ИСТИНА ,
naturalSpline() возвращает интеграл каждого натурального сплайна
основа.

 nsMat <- naturalSpline(x, узлы = узлы, перехват = ИСТИНА)
insMat <- naturalSpline(x, узлы = узлы, перехват = ИСТИНА, интеграл = ИСТИНА)
пар (mfrow = c (1, 2))
matplot(x, nsMat, type = "l", ylab = "Основа")
matplot(x, insMat, type = "l", ylab = "Интегралы")

Неотрицательные натуральные кубические сплайны (слева) и
соответствующие интегралы (справа).

 stopifnot(is_equivalent(nsMat, deriv(insMat)))

Подобно bernsteinPoly() , можно указать аргумент
производных в naturalSpline() или используйте
соответствующий метод deriv() для получения производных от
сплайновые базисные функции.

 d1nsMat <- naturalSpline(x, узлы = узлы, перехват = ИСТИНА, производные = 1)
d2nsMat <- производное (nsMat, 2)
пар (mfrow = c (1, 2))
matplot(x, d1nsMat, type = "l", ylab = "Первое производное")
matplot(x, d2nsMat, type = "l", ylab = "Вторые производные")

Производные натуральных кубических сплайнов.

Оценка новых значений с помощью

прогнозирования

Методы для сплайнов2 объектов, отправленных
общая функция , предсказывающая , будет полезна, если мы хотим
оцените объект сплайна при возможных новых значениях \(x\). Например, мы можем оценить
значение объекта I-сплайнов в предыдущем примере 0,275, 0,525,
и 0,8 соответственно следующим образом:

 new_x <- c(0,275, 0,525, 0,8)
имена(new_x) <- paste0("x=", new_x)
предсказать(isMat, new_x) 
 ## 1 2 3 4 5 6
## x=0,275 0,9994213 0,7730556 0,2310764 0,0000000 0,000000 0,000
## x=0,525 1,0000000 1,0000000 0,9765625 0,2696429 0,000625 0,000
## x=0,8 1,0000000 1,0000000 1,0000000 0,9428571 0,580000 0,125

С технической точки зрения, методы берут всю необходимую информацию, такую ​​как
как узлов , градусов , перехват ,
т. д., из атрибутов исходных объектов и вызвать соответствующие
функция автоматически для этих новых значений \(x\). Следовательно
прогнозировать методы не будут применимы, если эти атрибуты
как-то теряются после некоторых операций.

Ссылка

Де Бур, Карл. 1978. Практическое руководство по сплайнам . Том. 27. Новый
Йорк: Springer-verlag. https://doi.org/10.1002/zamm.19800600129.

Мейер, Мэри С. 2008. «Вывод с использованием регрессии с ограничением формы
Сплайны». Анналы прикладной статистики 2 (3):
1013–33. https://doi.org/10.1214/08-aoas167.

Пигл, Лес и Уэйн Тиллер. 1997. НУРБС
Книга . 2-е изд. Springer Science & Business Media.

Рамзи, Джеймс О. 1988. «Сплайны монотонной регрессии в
Действие." Статистическая наука 3 (4): 425–41. https://doi.org/10.1214/ss/1177012761.

Ван, Цзяндиан и Суджит К. Гош. 2012. «Форма ограничена
Непараметрическая регрессия с Бернштейном
Полиномы». Вычислительная статистика и данные
Анализ 56 (9): 2729–41.

в чем преимущество b-сплайнов перед другими сплайнами?

спросил

Изменено
6 месяцев назад

Просмотрено
2к раз

$\begingroup$

Я только читал, что это связано с числовыми причинами, например. на http://einspline.sourceforge.net/background.shtml, но я действительно не понимаю.
Может кто-нибудь объяснить это более просто?
Потому ли, что они состоят из линейных комбинаций? Если да, то почему/как это преимущество?

  • шлицы

$\endgroup$

3

$\begingroup$

Сплайны — это большой класс методов.

Метод B-сплайнов — это простой способ взять одну коварианту и расширить ее таким образом, чтобы она охватывала множество всех функций, являющихся полиномами степени $d$ между всеми заданными узлами и $d-1$ дифференцируемыми повсюду. они не только способ добиться такого расширения ковариаты, но любое другое расширение будет охватывать точно такой же набор функций, а B-сплайны имеют некоторые хорошие числовые свойства, поэтому если вам нужны сплайны, которые соответствуют этим условиям гладкости , есть не веская причина не использовать B-шлицы.

B-сплайны особенно популярны, потому что они очень просты и могут быть легко подключены к любой регрессионной модели без какого-либо редактирования модели для создания нелинейных эффектов без какого-либо специального редактирования программного обеспечения.

Но есть много других типов сплайнов, которые вы можете использовать. Вот некоторые из них:

  • М-сплайны: сплайны, охватывающие строго положительные функции
  • I-сплайны: сплайны, охватывающие строго монотонные функции
  • Натуральные сплайны: сплайны, первая производная которых постоянна вне узлов
  • P-сплайны: сплайны, производные которых оштрафованы для обеспечения
    гладкость (также известная как сглаживание сплайнов)

Обратите внимание, что сплайны M+I представляют собой особый случай; если вы хотите их использовать, B-сплайны просто не подходят. Естественные сплайны на самом деле являются подмножеством B-сплайнов. P-сплайны обладают некоторыми очень хорошими свойствами, но в целом требуют специальной программной реализации.