Содержание
Каталог проекта «Лекало архитектора»
В наличии 1 шт.
В корзину
↻
Условия доставки
| Издательство |
TATLIN |
|---|---|
| Год издания | 2019 |
| Переплет | Мягкий |
| Страниц | 82 |
| Формат | 290х110 мм |
| Язык | Русский |
| ISBN |
978-5-00075-179-4 |
| Артикул |
1108798 |
- О книге
- Об издательстве
Лекало — фигурная линейка для вычерчивания кривых линий. Инструмент позволяет относительно точно строить участки эллипсов, парабол, гипербол, различных спиралей. Мало кто знает, что кроме чертёжных лекал, есть ещё лекало измерения межзрачкового расстояния, парикмахерское лекало, лекало ремней, лекало копыта, офицерское лекало и даже лекало для измерения зоны антибиотикочувстительности, нет лишь лекала архитектора. Кроме одного. В 1984 году знаменитый итальянский архитектор Алессандро Мендини (1931–2019) создал своё персональное лекало мendini-graph, задачей которого была фиксация в наборе линий и двухмерных элементов шаблонов и образцов мастера. Предполагалось, что использование такого лекала даст возможность любому художнику безошибочно создавать проекты, основой которых будет почерк Мендини. Несмотря на то, что в графике лекала был применён обычный геометрический набор — треугольники, круги, квадраты — их последовательность, ритм и пропорции создали уникальную графическую композицию, характеризующую творчество выдающегося архитектора. Попытка объективизации субъективного начала Мастера не удалась, но мир пополнился ещё одним шедевром художника, который показался некоторым критикам бессмысленным, но давший его автору возможность переосмыслить своё творчество.
Инструмент позволяет относительно точно строить участки эллипсов, парабол, гипербол, различных спиралей. Мало кто знает, что кроме чертёжных лекал, есть ещё лекало измерения межзрачкового расстояния, парикмахерское лекало, лекало ремней, лекало копыта, офицерское лекало и даже лекало для измерения зоны антибиотикочувстительности, нет лишь лекала архитектора. Кроме одного. В 1984 году знаменитый итальянский архитектор Алессандро Мендини (1931–2019) создал своё персональное лекало мendini-graph, задачей которого была фиксация в наборе линий и двухмерных элементов шаблонов и образцов мастера. Предполагалось, что использование такого лекала даст возможность любому художнику безошибочно создавать проекты, основой которых будет почерк Мендини. Несмотря на то, что в графике лекала был применён обычный геометрический набор — треугольники, круги, квадраты — их последовательность, ритм и пропорции создали уникальную графическую композицию, характеризующую творчество выдающегося архитектора. Попытка объективизации субъективного начала Мастера не удалась, но мир пополнился ещё одним шедевром художника, который показался некоторым критикам бессмысленным, но давший его автору возможность переосмыслить своё творчество.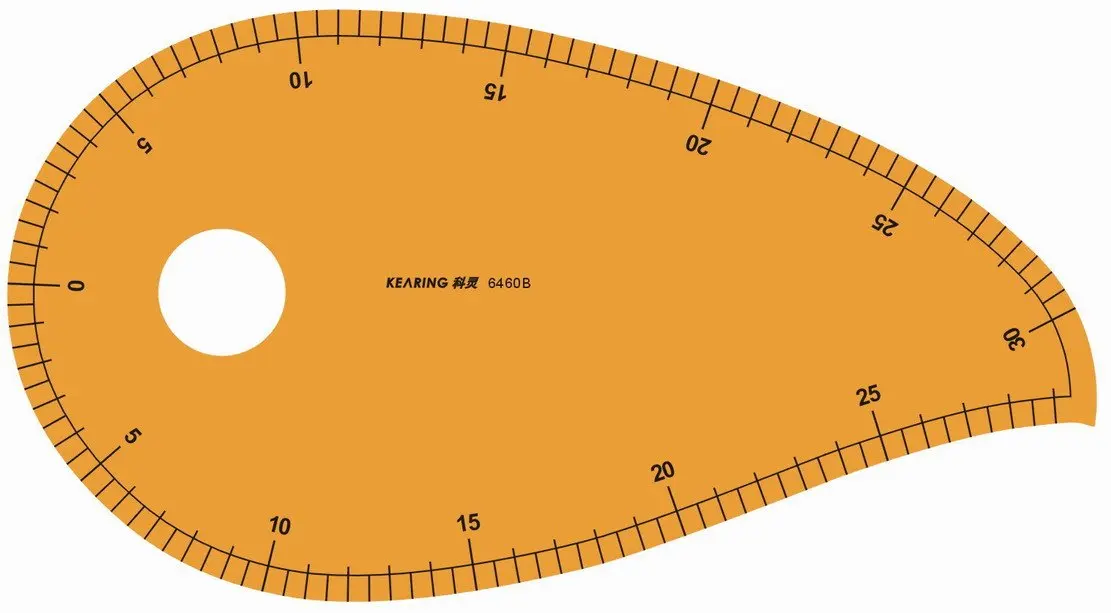 Опираясь на созданный Мастером прецедент, главный редактор издательства TATLIN Эдуард Кубенский предложил группе современных российских архитекторов разработать свои авторские лекала, состоящие из набора двухмерных элементов, наиболее часто используемых ими при работе над своими проектами. В качестве личного лекала куратор предложил криминалистическую линейку, используемую при обмере архитектурных объектов. С 26 декабря 2018 года по 3 февраля 2019 года в Музее архитектуры им. А. В. Щусева в Москве прошла выставка проекта «Лекало архитектора». Партнерами проекта выступили компании Arch-Skin, Laminam, Solo Офисные интерьеры и ВТБ–Инжиниринг. Данное издание является каталогом этого проекта.
Опираясь на созданный Мастером прецедент, главный редактор издательства TATLIN Эдуард Кубенский предложил группе современных российских архитекторов разработать свои авторские лекала, состоящие из набора двухмерных элементов, наиболее часто используемых ими при работе над своими проектами. В качестве личного лекала куратор предложил криминалистическую линейку, используемую при обмере архитектурных объектов. С 26 декабря 2018 года по 3 февраля 2019 года в Музее архитектуры им. А. В. Щусева в Москве прошла выставка проекта «Лекало архитектора». Партнерами проекта выступили компании Arch-Skin, Laminam, Solo Офисные интерьеры и ВТБ–Инжиниринг. Данное издание является каталогом этого проекта.
Из истории
Издательство было основано в 2001 году в Екатеринбурге выпускниками Уральской государственной архитектурно-художественной академии Эдуардом и Татьяной Кубенскими– там до сих пор находится головной офис компании, к которому прибавился филиал в Москве. Спектр интересующих издательство тем столь же обширен, сколь широка география России: TATLIN публикует и карты Нижнего Новгорода образца 1960–1990 годов, и плакаты Дома сотрудников Наркомфина, и труды важнейших деятелей советского модернизма вроде Евсея Перченкова и Александра Шипкова.
Как раз-таки за свою многогранность и вневременную ценность TATLIN получает награды – за более чем двадцатилетнюю историю издательство становилось лауреатом многих отечественных и международных премий, в том числе от Союза архитекторов России и Международной академии архитектуры. На базе издательства и с его подачи проводится масса мероприятий, выставок и фестивалей, ставящих целью популяризацию творческого наследия советской архитектуры.
Книжные серии
В издательском портфеле TATLIN – книги по архитектуре советского модернизма, монографии современных деятелей архитектуры России и их советских предшественников, уникальные плакаты и путеводители по местам силы советской архитектуры, а еще и макеты, планы, карты и много прикладных вещей для ценителей и практикующих деятелей! От имен и пространств веет историчной величавостью – Ларин, Прудникова, Гинзбург, Явейн, Музей истории космонавтики, Белоусовы, Наседкин, Дом Мельникова, Самара 1920-1940 годов, Травуш… Но это не значит, что знакомство с ними стоит откладывать из-за тяжести или монолитности! Наоборот, издания TATLIN ориентированы на то, чтобы помочь читателям свести знакомство с главными персоналиями и явлениями, рассмотреть завитки творческих карьер и детали зданий. Для этого на базе издательства функционирует и одноименный журнал, не единожды признававшийся лучшим архитектурным журналом России.
Для этого на базе издательства функционирует и одноименный журнал, не единожды признававшийся лучшим архитектурным журналом России.
За что мы любим TATLIN?
За то, что TATLIN утоляет наш бесконечный интерес к временам ушедшим, но оставшимся в нашей жизни в виде архитектурных памятников и людей, которые определили внешний вид наших родных городов. Возможность окунуться в пространство Самары середины прошлого века, рассмотреть в деталях Шаболовскую радиобашню или собрать конструктивистский гроб Малевича – как можно отказываться от таких заманчивостей?
Подписка на рассылку
Раз в месяц будем присылать вам обзоры книг, промокоды и всякие-разные новости
Лекала и выкройки: в чём разница между ними
Мир шитья полон разнообразных терминов, в которых не всегда бывает просто разобраться, особенно новичку. Например, многие часто используют слова лекало и выкройка как взаимозаменяемые. И даже поисковые системы этим грешат — вбив в строку поиска слово «выкройки», можно обнаружить там лекала для пошива одежды или наоборот. В этой статье мы постараемся разобраться, чем они отличаются друг от друга.
В этой статье мы постараемся разобраться, чем они отличаются друг от друга.
Мир шитья полон разнообразных терминов, в которых не всегда бывает просто разобраться, особенно новичку. Например, многие часто используют слова лекало и выкройка как взаимозаменяемые. И даже поисковые системы этим грешат — вбив в строку поиска слово «выкройки», можно обнаружить там лекала для пошива одежды или наоборот. В этой статье мы постараемся разобраться, чем они отличаются друг от друга.
Что такое выкройка и в чём её особенности
Выкройка — это базовый трафарет будущего изделия, выполненный на бумаге, кальке, отрезке полиэтилена, куске кожи и пр. В ней содержится множество информации в виде цифр, символов, надписей, букв. Являясь образцом для создания одежды, выкройки обычно применяются при пошиве единичных заказов. В неё можно вносить изменения и применять повторно.
Применение
Для чего нужны выкройки? При создании красивой и комфортной одежды, например, джинсов предварительно составляется эскиз — все детали продумываются и постепенно дорабатываются. На этом этапе также выполняется моделирование. Именно здесь и необходим трафарет, который содержит всю нужную информацию, в том числе мерки, снятые с фигуры будущего владельца вещи.
На этом этапе также выполняется моделирование. Именно здесь и необходим трафарет, который содержит всю нужную информацию, в том числе мерки, снятые с фигуры будущего владельца вещи.
Есть множество базовых выкроек, в которые можно вносить изменения. Например, используя трафарет для платья с рукавами-фонариками, его можно доработать — уменьшить длину или даже превратить в жакет.
Применение выкроек позволяет ускорить процесс кроя, заранее узнать необходимый метраж для пошива, обеспечить идеальную посадку по фигуре. Образцы требуются не для всех изделий — такие простые вещи как прямоугольные тканевые сумки, простые майки или прямые сарафаны без пояса можно сшить без них.
Материалы для создания
При изготовлении выкройки применяются разные материалы. Самый популярный вариант — калька. Это тонкая полупрозрачная бумага, которая продаётся в рулонах. Перед использованием её обычно распрямляют с помощью утюга.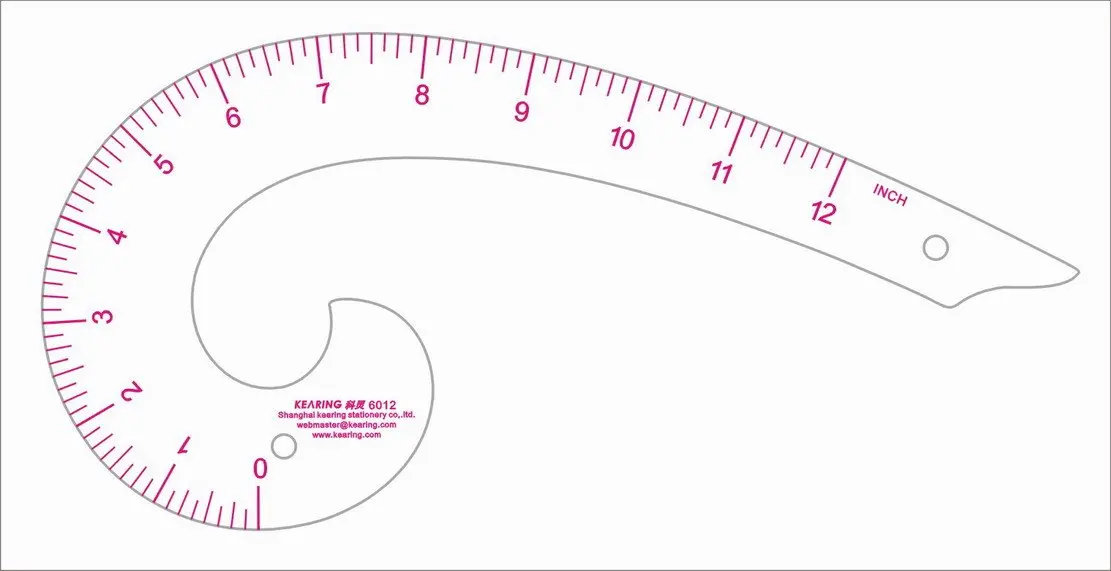 За счёт высокой прозрачности и относительной прочности с этим материалом легко работать. Тем не менее возможны и другие варианты, например:
За счёт высокой прозрачности и относительной прочности с этим материалом легко работать. Тем не менее возможны и другие варианты, например:
- Картон. Прочный, долговечный материал. Срезы рекомендуется обклеить скотчем, чтобы защитить трафареты от истирания.
- Ткань. Разглаженная чистая ткань также часто выполняет роль материала для создания образцов.
- Миллиметровка. Это специальная чертёжная бумага, размеченная на клетки. Позволяет создавать точные детали без применения измерительных инструментов.
- ПВХ-плёнка. Устойчива к влаге, долговечна. Все необходимые разметки можно наносить с помощью маркера.
Также выкройки для одежды можно сделать из обычной бумаги, правда для повышения прочности её рекомендуется обклеить скотчем.
Какие инструменты нужны для работы
Также при создании выкроек нужны специальные швейные инструменты, без которых невозможно создать качественный трафарет. А именно:
А именно:
- Портновское лекало. Инструмент, внешне напоминающий многоуровневую линейку, однако обладающий более сложной системой измерения. С его помощью швеи чертят кривые — линии боковин, пройм и пр.
- Сантиметр. Гибкая измерительная лента, необходимая для снятия мерок. Рекомендуется приобретать двухсторонний инструмент, на одной стороне которого сантиметры, а на другой — дюймы.
- Линейки. Обычные линейки тоже нужны в работе, а именно — средняя, большая (метровая) и угольник. Лучше обратить внимание на прозрачные пластиковые линейки, поскольку с ними гораздо удобнее работать.
- Шаблоны. Для создания некоторых мелких деталей можно приобрести готовые швейные шаблоны. Например, для карманов. Они помогут ускорить работу.
- Принадлежности для нанесения разметок. Это может быть мел, уголь, маркер, карандаш.
Полный список зависит от опыта работы швеи и её предпочтений. Как правило, с годами у каждого складывается индивидуальный набор привычных инструментов, поэтому приведённый перечень является ознакомительным.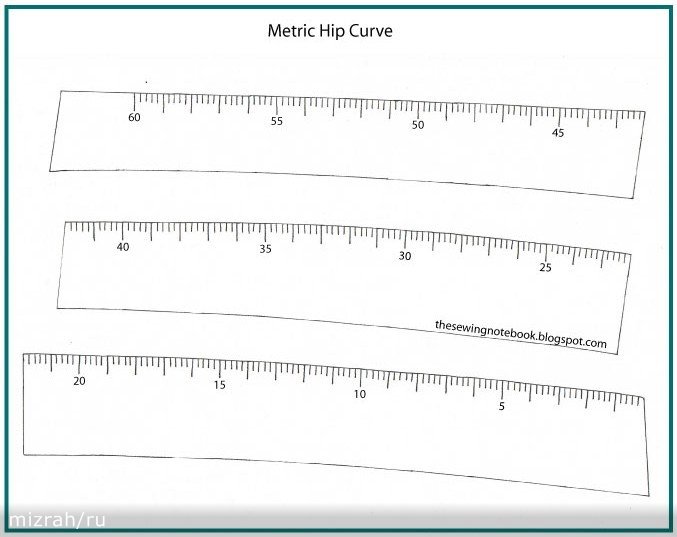
Что такое лекало
Лекало также представляет собой полностью готовый шаблон для пошива одежды, но, в отличие от выкроек, к ним гораздо больше требований. Трафарет содержит большое количество точных обозначений и разметок, специальные знаки, информацию о материале, типе швов и пр. Их изготавливают из более износостойких материалов, в основном из крафтового или электрокартона.
Это швейные детали, полностью готовые к раскрою, в которые уже невозможно внести никакие изменения. В состав лекал входят все детали будущей вещи, включая верхнюю часть, подклад, рукава, отступы и т.д., а также техническое задание для его пошива.
Где и когда используют лекала
Для чего нужны лекала? Их используют для пошива большой партии изделий, например, на крупных швейных фабриках. Лекала представляют собой согласованный и утверждённый образец, в точности соответствующий определённым техническим параметрам.
Как правило, образцы используются многократно, и многие производители хранят наиболее популярные из них годами.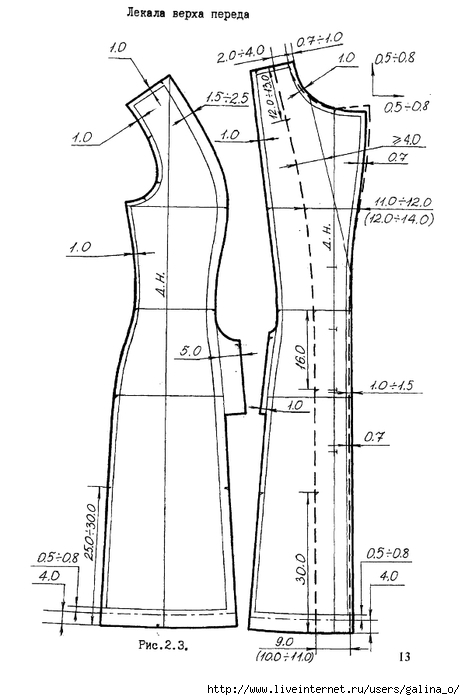 Есть даже так называемые эталонные лекала, с помощью которых проверяют точность новых трафаретов. Для создания комплекта лекал требуется огромный труд, поскольку бывает достаточно сложно привести их в соответствие строгим техническим требованиям.
Есть даже так называемые эталонные лекала, с помощью которых проверяют точность новых трафаретов. Для создания комплекта лекал требуется огромный труд, поскольку бывает достаточно сложно привести их в соответствие строгим техническим требованиям.
В чём разница между лекалом и выкройкой
Подведём итоги — в чём же заключается разница между выкройками и лекалами?
- Масштаб производства. Выкройки обычно используются для создания одного или нескольких изделий, лекала — для большой партии одежды (и, как правило, не одной).
- Изменяемость. Выкройки можно корректировать, а лекала — нет.
- Долговечность. Швейные лекала создаются из максимально плотных и долговечных материалов, в случае с выкройками выбор материалов основы гораздо больше.
- Точность. В лекалах присутствует огромное количество информации, вплоть до направления нитей. На выкройках информации значительно меньше.
Другими словами, нельзя прийти на производство с выкройками и попросить сшить партию изделий, например, джинс.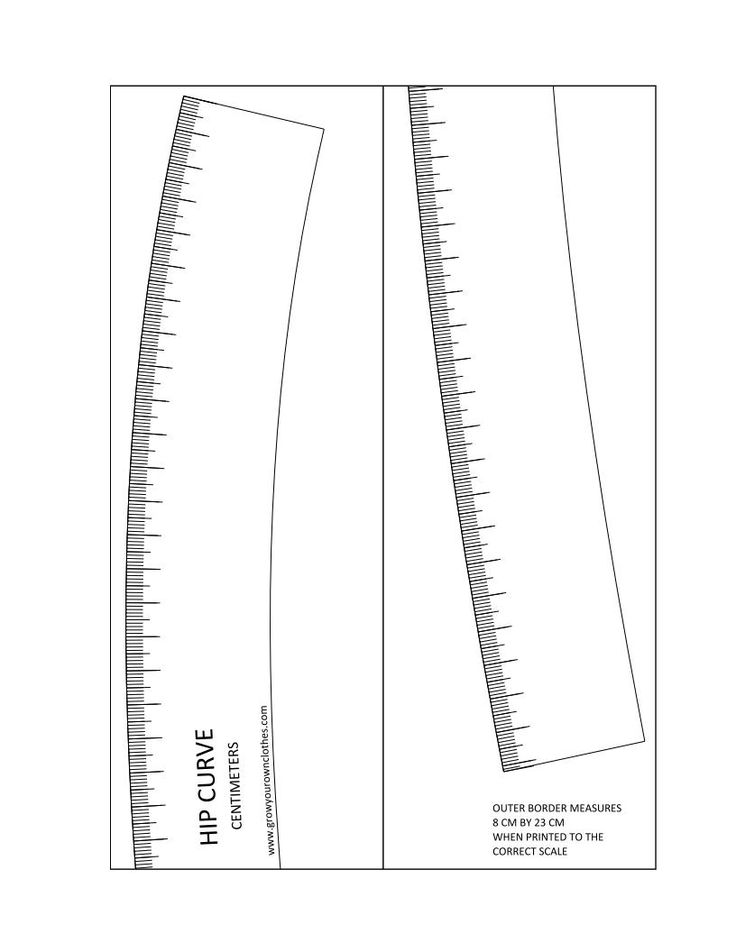 От вас потребуют создание лекал. Вывод — между этими двумя понятиями всё же есть ощутимая разница, и их нельзя использовать как синонимы.
От вас потребуют создание лекал. Вывод — между этими двумя понятиями всё же есть ощутимая разница, и их нельзя использовать как синонимы.
Источник фото: a-soul.ru
Что такое закономерности в математике? Определение, типы, примеры, факты
Определение
В математике шаблон определяется как последовательность повторяющихся объектов, фигур или чисел. Мы можем связать паттерн с любым типом события или объекта. У шаблона есть правило, которое говорит нам, какие объекты принадлежат шаблону, а какие не принадлежат шаблону. Давайте рассмотрим несколько примеров узоров:
На приведенном выше изображении соблюдается правило, согласно которому круг находится в нечетных местах, а прямоугольник — в четных. Значит, следующей цифрой в паттерне будет:
Узоры окружают нас повсюду. Мы можем найти рисунок на деревьях, в оконных рамах, на полу, в нашей одежде и т. д. Одним из таких примеров из реальной жизни является рисунок зебры.
Шаблоны могут быть конечными и бесконечными.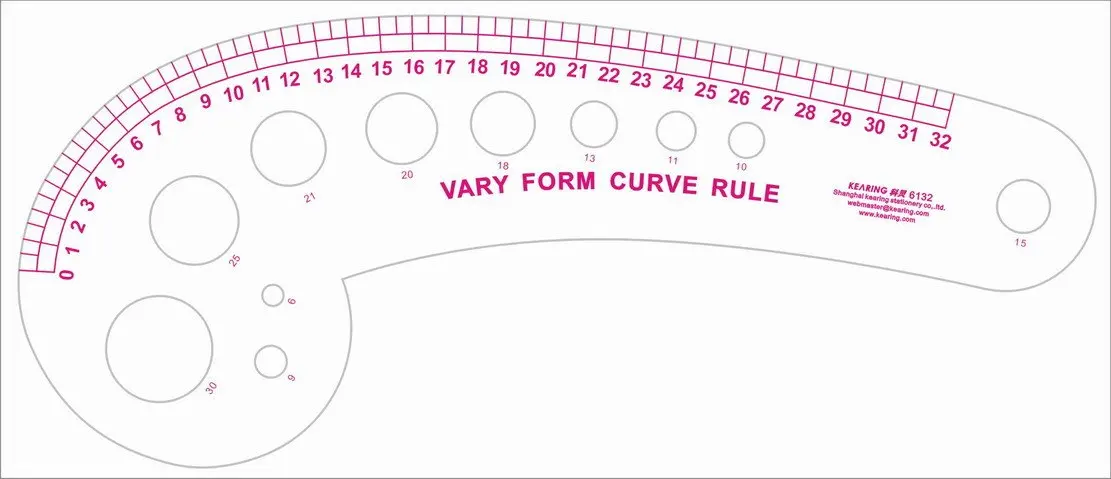
Родственные игры
Конечные шаблоны
Конечный шаблон — это конечная последовательность, в которой мы знаем первый член и последний член.
Например: В шаблоне 3, 6, 9, 12, 15 первый член равен 3, а последний член равен 15.
Связанные листы
Бесконечные шаблоны
Бесконечный шаблон — это последовательность, в которой мы знаем первый член, но не знаем последний член.
Например: В схеме 3, 6, 9, 12, 15, 18, ………; первый член равен 3, но мы не знаем, где остановится шаблон.
Правила шаблона
Для создания полного шаблона необходимо учитывать определенный набор правил. Чтобы применить эти правила, мы должны сначала понять природу последовательности и разницу между двумя последовательными числами, данными в шаблоне. Требуется некоторое количество догадок, а затем мы проверяем, работает ли правило во всем шаблоне.
Шаблоны могут быть сформированы с использованием трех категорий:
Повторяющийся шаблон
Тип шаблона, в котором правило повторяется снова и снова, называется повторяющимся шаблоном.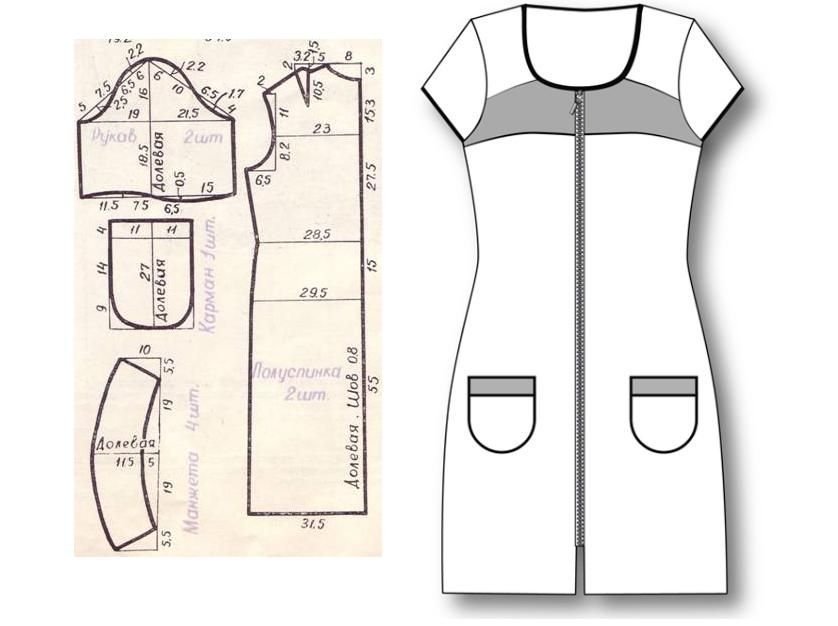 Обычно это буквы и формы.
Обычно это буквы и формы.
Растущий шаблон
В растущем шаблоне числа располагаются в возрастающей форме или каждое число больше предыдущего, тогда такой шаблон называется растущим шаблоном. Пример: 44, 50, 56, 62, …
Шаблон сжатия
В схеме уклонения числа располагаются в порядке убывания или каждое число меньше предыдущего. Пример: 40, 35, 30, 25 …
Типы шаблонов
Существует 3 типа шаблонов:
- Шаблон формы
- Шаблон письма
- Образец номера
1. Шаблон формы
Когда группа фигур повторяется, шаблон или последовательность называется шаблоном формы. Шаблоны фигур следуют определенной последовательности или порядку фигур, т. Е. Они повторяются. Формы могут быть простыми, такими как круги, квадраты, прямоугольники, треугольники и т. д., или другими объектами, такими как стрелки, цветы, луны и звезды.
Например:
В приведенном выше шаблоне стрелка поворачивается на 90° и меняет свой цвет.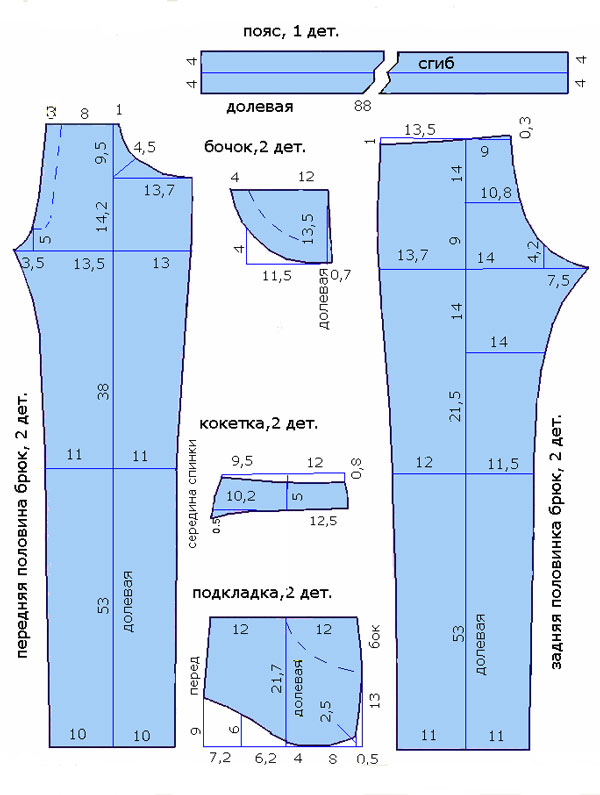 Или мы можем сказать, что каждая цветная фигура повторяется после двух фигур.
Или мы можем сказать, что каждая цветная фигура повторяется после двух фигур.
2. Образец букв
Последовательность, состоящая из букв или букв английского алфавита, называется образцом букв. Образец букв устанавливает общую связь между всеми буквами.
Например: A, C, E, G, I, K, M…
В приведенном выше шаблоне после каждого алфавита удалена одна буква.
3. Числовой шаблон
Наиболее распространенным типом числового шаблона в математике является числовой шаблон, в котором список чисел следует определенной последовательности, основанной на правиле.
Существуют различные типы числовых шаблонов:
Арифметический шаблон
Другое название арифметического шаблона — алгебраический шаблон. В таком шаблоне последовательности основаны на добавлении или вычитании терминов. Если мы знаем два или более термина в последовательности, мы можем использовать сложение или вычитание, чтобы найти арифметическую закономерность.
Пример 1. В шаблоне 65, 64, 63, 62, 61 мы вычитаем последовательные числа на 1 или каждое число уменьшается на 1.
Пример 2. В приведенном ниже шаблоне:
Каждое число увеличивается на 5.
Геометрический узор
Последовательность чисел, основанная на умножении и делении, называется геометрическим узором. Если нам даны два или более числа в последовательности, мы можем легко найти неизвестные числа в образце, используя операции умножения и деления.
Пример 1: Симран имеет $\$10$ в качестве сбережений в первый месяц. Во второй месяц ее сбережения удвоились. Итак, теперь у нее 10 x 2 = $\$$20. Опять же, на третьем месяце ее сбережения удвоились. Теперь у нее 20 х 2 = $\$40. Таким образом, схема здесь $\$$10, $\$$20, $\$$40.
Пример 2. В приведенном ниже шаблоне каждое число делится на 5.
3125, 625, 125, 25, 5
Шаблон Фибоначчи
Последовательность чисел, в которой каждое число в последовательности полученный путем сложения двух предыдущих чисел вместе, известен как ряд или паттерн Фибоначчи. Эта последовательность начинается с 0 и 1. Мы складываем два числа, чтобы получить третье число в последовательности.
Эта последовательность начинается с 0 и 1. Мы складываем два числа, чтобы получить третье число в последовательности.
Последовательность 0, 1, 1, 2, 3, 5, 8, 13 является фигурой Фибоначчи.
Здесь используется следующий шаблон: 0 + 1 = 1, 1 + 1 = 2 , 1 + 2 = 3 , 2 + 3 = 5, 3 + 5 = 8.
Образец треугольного числа из чисел в форме равностороннего треугольника, расположенных в серии или последовательности, известен как треугольный образец числа. Числа в треугольном узоре расположены в последовательности 1, 3, 6, 10, 15, 21, 28, 36, 45 и так далее. 93$…= 1, 8, 27, 64, 125…
Приведенные выше числовые шаблоны являются наиболее часто используемыми. Числовых моделей больше. Например: шаблон нечетных чисел, шаблон четных чисел, шаблон кратных чисел и т. д.
Решаемые примеры
Пример 1: Какой будет следующая фигура в шаблоне?
Решение : Узор состоит из 2 овалов и квадрата, повторяется один и тот же узор. Следующей фигурой в шаблоне будет овал, т. е.:
Следующей фигурой в шаблоне будет овал, т. е.:
Пример 2. Заполните шаблон: 10, 13, 16, 19, ____, ____
Решение :
Итак, следующие числа будут 19 + 3 = 2 2, 22 + 3 = 25
Пример 3. Заполните шаблон: AB, BC, CD, DE, ____, ____
Решение : Первый член представляет собой комбинацию первого и второго алфавитов. Второй термин представляет собой комбинацию второго и третьего алфавитов. Третий термин представляет собой комбинацию третьего и четвертого алфавитов. Четвертый термин представляет собой комбинацию четвертого и пятого терминов.
Точно так же следующие два термина будут EF и FG.
Практические задачи
1
Обратите внимание на шаблон: 2, 4, 6, 8, 10, 12… Какой это тип шаблона?
Образец в порядке возрастания
Образец, кратный 2
Образец четных чисел
Все эти
Правильный ответ: Все эти
Каждое число больше предыдущего. 2, 4, 6, 8 и т. д. являются числами, кратными 2,
2, 4, 6, 8 и т. д. являются числами, кратными 2,
. Кроме того, каждое число является последовательным четным числом.
2
Название типа шаблона: 1, 3, 6, 10, 15
Конечный шаблон
Треугольный шаблон чисел
Оба A и B
Ни один из этих
Правильный ответ: и А, и Б.
Мы знаем первый и последний член. Также шаблон можно описать как 0 + 1 = 1, 1 + 2 = 3, 3 + 3 = 6, 6 + 4 = 10, 10 + 5 = 15 и так далее.
3
Какой термин будет следующим в шаблоне? A, AB, ABC, ABCD, _____
ABCDF
ABCDE
ACDEF
ABBBC
Правильный ответ: ABCDE
Схема состоит в том, что каждый последующий алфавит добавляется к предыдущему алфавиту. Итак, следующий член шаблона — ABCDE.
4
Какое из следующих чисел является лишним в последовательности: 8, 27, 125, 216, 343, 1331
216
125
343
90 004 1331
Правильный ответ: 216
Кроме 216 , все числа являются кубом простых чисел. Итак, 216 — это лишний.
Итак, 216 — это лишний.
Часто задаваемые вопросы
Что такое шаблонное правило?
Числовой шаблон может быть создан на основе формулы или правила, известного как правило шаблона. Правила шаблона могут использовать одну или несколько математических операций для описания отношения между последовательными числами в шаблоне.
Как шаблоны используются в реальной жизни?
Некоторые примеры применения паттернов в реальной жизни:
1. Музыка основана на паттернах.
2. Создание ранголи основано на шаблонах.
3. В волнах, молнии и т. д. можно обнаружить некоторые естественные узоры.
Почему узоры важны?
Шаблоны помогают предсказать, что будет дальше. Они также помогают детям в изучении логических связей и навыков рассуждения.
Закономерности в математике (определение, типы и примеры)
Математика — это числа. Он включает в себя изучение различных моделей. Существуют различные типы паттернов, такие как числовые паттерны, паттерны изображений, логические паттерны, паттерны слов и т. д. Цифровые паттерны очень распространены в математике. Они хорошо знакомы студентам, которые часто изучают математику. В частности, числовые закономерности повсюду в математике. Все шаблоны чисел — это предсказания. В этой статье мы обсудим, что такое шаблон, а также различные типы шаблонов, такие как арифметический шаблон, геометрический шаблон и множество решенных примеров.
Существуют различные типы паттернов, такие как числовые паттерны, паттерны изображений, логические паттерны, паттерны слов и т. д. Цифровые паттерны очень распространены в математике. Они хорошо знакомы студентам, которые часто изучают математику. В частности, числовые закономерности повсюду в математике. Все шаблоны чисел — это предсказания. В этой статье мы обсудим, что такое шаблон, а также различные типы шаблонов, такие как арифметический шаблон, геометрический шаблон и множество решенных примеров.
Содержание:
- Определение
- Типы числовых шаблонов
- Арифметический шаблон
- Геометрический узор
- Паттерн Фибоначчи
- Правила
- Типы
- Примеры
- Часто задаваемые вопросы
Шаблоны в математике
В математике шаблон — это повторяющееся расположение чисел, форм, цветов и т. д. Шаблон может быть связан с любым типом события или объекта. Если набор чисел связан друг с другом по определенному правилу, то это правило или способ называется шаблоном. Иногда шаблоны также называют последовательностями. Шаблоны конечны или бесконечны в числах.
Если набор чисел связан друг с другом по определенному правилу, то это правило или способ называется шаблоном. Иногда шаблоны также называют последовательностями. Шаблоны конечны или бесконечны в числах.
Например, в последовательности 2,4,6,8,?. каждое число увеличивается на 2. Итак, последнее число будет 8 + 2 = 10.
Несколько примеров числовых шаблонов:
Шаблон четных чисел -: 2, 4, 6, 8, 10, 1, 14, 16, 18, …
Шаблон нечетных чисел -: 3, 5, 7, 9, 11, 13, 15, 17, 19, …
Числа Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, … и так далее.
Шаблоны номеров
Список чисел, следующих за определенной последовательностью, известен как шаблоны или шаблоны чисел. Различные типы числовых шаблонов: алгебраический или арифметический шаблон, геометрический шаблон, шаблон Фибоначчи и так далее. Теперь давайте посмотрим на три разных шаблона здесь.
Арифметический шаблон
Арифметический шаблон также известен как алгебраический шаблон. В арифметическом шаблоне последовательности основаны на сложении или вычитании членов. Если заданы два или более термина в последовательности, мы можем использовать сложение или вычитание, чтобы найти арифметический шаблон.
В арифметическом шаблоне последовательности основаны на сложении или вычитании членов. Если заданы два или более термина в последовательности, мы можем использовать сложение или вычитание, чтобы найти арифметический шаблон.
Например, 2, 4, 6, 8, 10, __, 14, __. Теперь нам нужно найти пропущенный член в последовательности.
Здесь мы можем использовать процесс сложения, чтобы выяснить недостающие термины в шаблонах.
В шаблоне используется правило «Добавьте 2 к предыдущему термину, чтобы получить следующий термин».
В приведенном выше примере возьмите второе слагаемое (4). Если мы добавим «2» ко второму члену (4), мы получим третий член 6.
Точно так же мы можем найти неизвестные элементы в последовательности.
Первый пропущенный член: Предыдущий член равен 10. Следовательно, 10+2 = 12.
Второй пропущенный член: Предыдущий член равен 14. Таким образом, 14+2 = 16
Следовательно, полный арифметический шаблон равен 2, 4, 6, 8, 10, 9.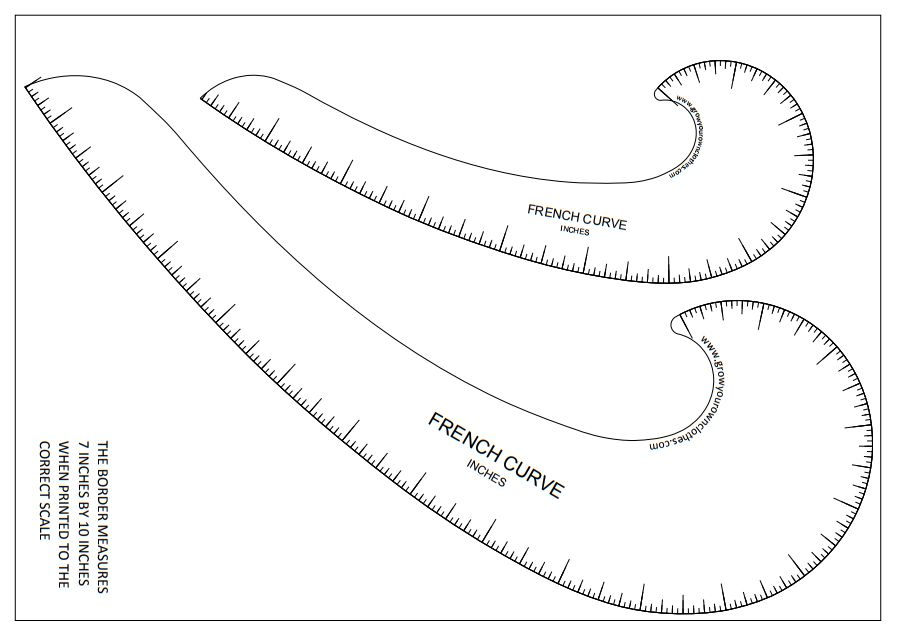 0352 12 , 14, 16 .
0352 12 , 14, 16 .
Геометрический узор
Геометрический узор определяется как последовательность чисел, основанная на операции умножения и деления. Подобно арифметическому шаблону, если в последовательности представлены два или более числа, мы можем легко найти неизвестные элементы в шаблоне, используя операции умножения и деления.
Например, 8, 16, 32, __, 128, __.
Это геометрический узор, так как каждый член последовательности можно получить, умножив 2 на предыдущий член.
Например, 32 — это третий член последовательности, которая получается путем умножения 2 на предыдущий член 16.
Точно так же мы можем найти неизвестные элементы в геометрической схеме.
Первый пропущенный член: Предыдущий член равен 32. Умножаем 32 на 2, получаем 64.
Второй пропущенный член: Предыдущий член равен 128. Умножаем 128 на 2, получаем 256.
Следовательно, полный геометрический рисунок равен 8, 16, 32, 64 , 128, 256 .
Паттерн Фибоначчи
Шаблон Фибоначчи определяется как последовательность чисел, в которой каждый член последовательности получается путем добавления двух членов перед ним, начиная с чисел 0 и 1. Шаблон Фибоначчи задается как 0, 1, 1, 2 , 3, 5, 8, 13, … и так далее.
Объяснение:
Третий член = Первый член + Второй член = 0+1 = 1
Четвертый член = второй член + Третий член = 1+1 = 2
Пятый член = Третий член + Четвертый член = 1+2 = 3 и так далее.
Правила шаблонов в математике
Чтобы построить шаблон, мы должны знать некоторые правила. Чтобы узнать о правиле для любого шаблона, мы должны понимать природу последовательности и разницу между двумя последовательными терминами.
Поиск пропущенного термина: Рассмотрим шаблон 1, 4, 9, 16, 25, ?. В этом шаблоне ясно, что каждое число является квадратом их номера позиции. Недостающий член имеет место при n = 6. Таким образом, если отсутствующий член равен x n, затем x n = n 2 . Здесь n = 6, тогда x n = (6) 2 = 36,
Здесь n = 6, тогда x n = (6) 2 = 36,
Правило различия: Иногда легко найти разницу между двумя последовательными терминами. Например, рассмотрим 1, 5, 9, 13,……. В этом типе шаблона сначала мы должны найти разницу между двумя парами последовательности. После этого найдите остальные элементы узора. В данной задаче разница между слагаемыми равна 4, т.е. если мы прибавим 4 и 1, то получим 5, а если прибавим 4 и 5, то получим 9и так далее.
Типы узоров
В дискретной математике у нас есть три типа шаблонов:
- Повторяющийся — Тип шаблона, в котором правило повторяется снова и снова, называется повторяющимся шаблоном.
- Растущий — Если числа представлены в возрастающей форме, то эта модель называется растущей. Пример 34, 40, 46, 52, …..
- Прогулы – В схеме прогулов числа указаны в убывающей форме. Пример: 42, 40, 38, 36 …..
Примеры арифметических и геометрических фигур
Пример 1:
Определите значение P и Q по следующему шаблону.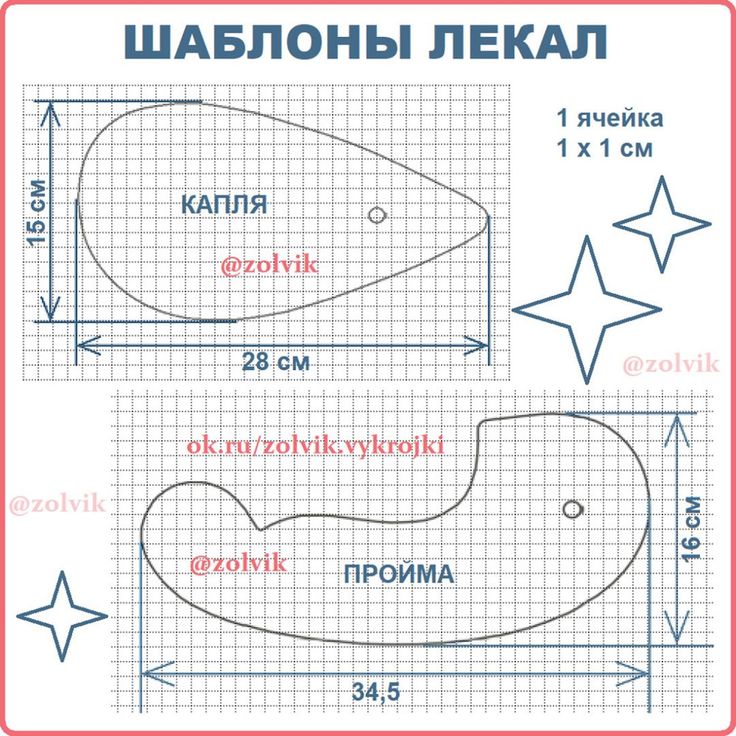
85, 79, 73, 67, 61, 55, 49, 43, П, 31, 25, Q.
Решение:
Данная последовательность: 85, 79, 73, 67, 61, 55, 49, 43, P, 31, 25, Q.
Здесь число уменьшается на 6
Предыдущее число Р равно 43. Значит, Р будет 43 – 6, Р = 37
Предыдущее число Q равно 25. Значит, Q будет 25 – 6, Q = 19
Следовательно, значение P равно 37, а Q равно 19.
Пример 2:
Определите значение A и B по следующему шаблону.
15, 22, 29, 36, 43, А, 57, 64, 71, 78, 85, Б.
Решение:
Данная последовательность: 15, 22, 29, 36, 43, А, 57, 64, 71, 78, 85, Б.
Здесь число увеличивается на +7
Предыдущее число А равно 43. Значит, А будет 43 + 7, А = 50
Предыдущее число B равно 85. Значит, B будет 85 + 7, B = 92
Следовательно, значение A равно 50, а B равно 92.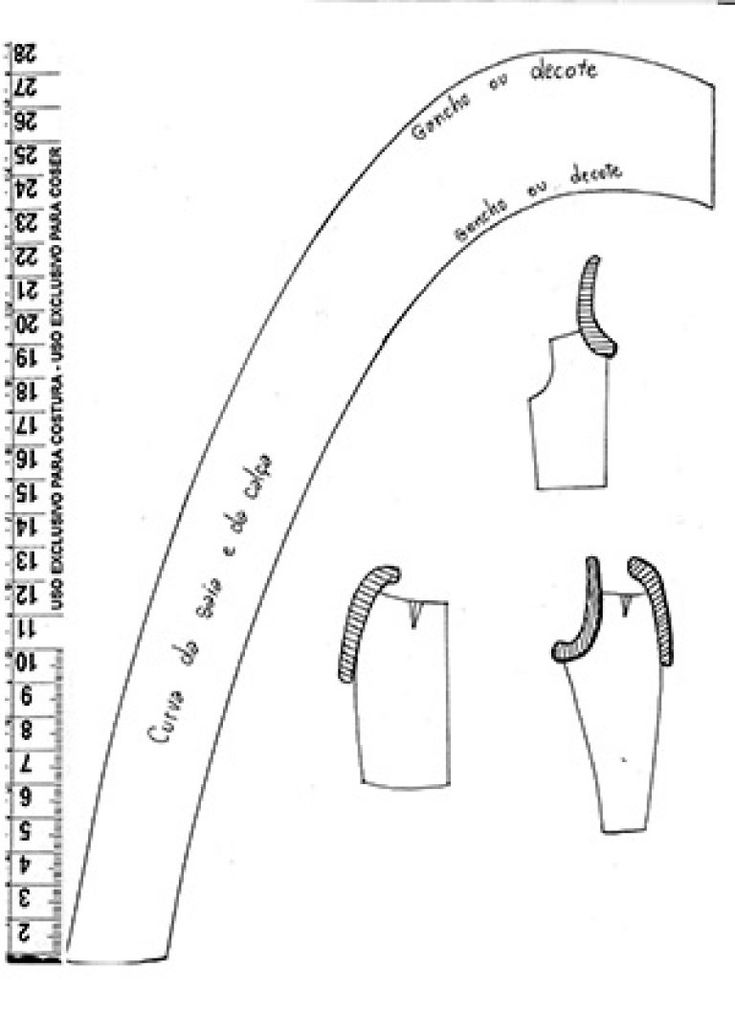
Пример 3:
Найдите недостающее значение в геометрической схеме: 120, 60, __, 15, __.
Решение:
Дано: Геометрический узор 120, 60, __, 15, __.
В этом геометрическом шаблоне используется правило: «Для получения следующего члена нужно разделить предыдущий член на 2».
(т.е.) 120/2 = 60
Тогда первый пропущенный член = 60/2 = 30
Второй пропущенный член = 15/2 = 7,5
Следовательно, геометрическая последовательность равна 120, 60, 30 , 15, 7,5 .
Часто задаваемые вопросы по шаблонам
Q1
Что понимают под шаблонами в математике?
В математике шаблон также известен как последовательность. Список чисел, упорядоченных по определенным правилам, называется шаблоном.
Q2
Укажите два разных типа числовых шаблонов.
Два разных типа числовых шаблонов:
Арифметический шаблон
Геометрический шаблон
Q3
Что называется числовым шаблоном?
Образец чисел устанавливает взаимосвязь между всеми числами.