Содержание
Пропорциональная
фигура презентация, доклад
Пропорциональная
фигура
ЦЕНТР ЮНОШЕСКОГО НАУЧНО-ТЕХНИЧЕСКОГО ТВОРЧЕСТВА
Педагог дополнительного образования
Щеголева Римма Раисовна
это отношение
каждой части тела
к другим частям
и ко всей фигуре в целом
ПРОПОРЦИЯ
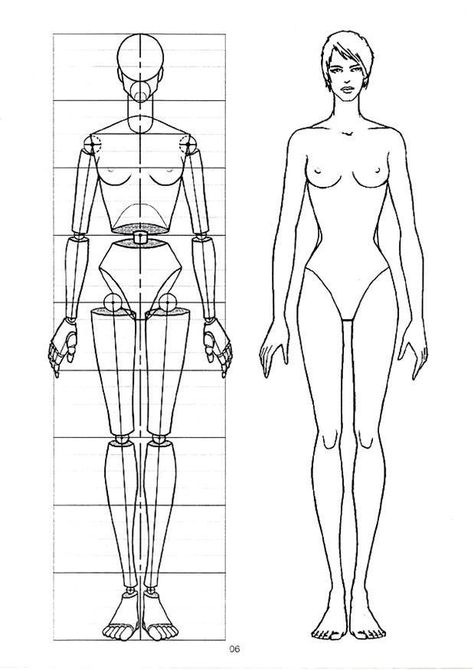
пропорциональная фигура
За модуль принимается размер головы
от темени до подбородка
схема условно-пропорциональной фигуры
За модуль принимается размер головы
от темени до подбородка
Рост равен 8 модулям
3
4
5
6
7
8
1
2
схема условно-пропорциональной фигуры
За модуль принимается размер головы
от темени до подбородка
Рост равен 8 модулям
Ширина талии равна 1 модулю
схема условно-пропорциональной фигуры
За модуль принимается размер головы
от темени до подбородка
Рост равен 8 модулям
Ширина талии равна 1 модулю
Ширина плеч и ширина бедер равна
1,5 модулям
схема условно-пропорциональной фигуры
За модуль принимается размер головы
от темени до подбородка
Рост равен 8 модулям
Ширина талии равна 1 модулю
Ширина плеч и ширина бедер равна
1,5 модулям
Линия талии делит фигуру в соотношении 3/5
схема условно-пропорциональной фигуры
За модуль принимается размер головы
от темени до подбородка
Рост равен 8 модулям
Ширина талии равна 1 модулю
Ширина плеч и ширина бедер равна
1,5 модулям
Линия талии делит фигуру в соотношении 3/5
Основание туловища находится ровно
посередине фигуры
схема условно-пропорциональной фигуры
За модуль принимается размер головы
от темени до подбородка
Рост равен 8 модулям
Ширина талии равна 1 модулю
Ширина плеч и ширина бедер равна
1,5 модулям
Линия талии делит фигуру в соотношении 3/5
Основание туловища находится ровно
посередине фигуры
Локоть находится посередине руки,
при опущенной руке – на уровне линии талии
схема условно-пропорциональной фигуры
За модуль принимается размер головы
от темени до подбородка
Рост равен 8 модулям
Ширина талии равна 1 модулю
Ширина плеч и ширина бедер равна
1,5 модулям
Линия талии делит фигуру в соотношении 3/5
Основание туловища находится ровно
посередине фигуры
Локоть находится посередине руки,
при опущенной руке – на уровне линии талии
Линия коленей находится посередине
расстояния от основания туловища до
основания ступней
Скачать презентацию
Идеальная фигура.
Женская антропометрия
Великий Леонардо да Винчи был одним из первых, кто изучил и дал определение идеальных параметров человеческого тела. Представленные им анатомические пропорции до сих пор изучают в школах искусства во всем мире. Из теории идеальных пропорций Леонардо да Винчи следует, что объемы груди, талии и бедер, взятые по отдельности, ничего не решают, все дело в их соотношении.
В современном обществе изменения параметров человеческого тела (антропометрические данные) пересматриваются через каждые 15 лет, т. к. за этот период в результате процесса акселерации происходят изменения размеров, пропорций и форм фигуры человека. Хорошо известные всем 90 – 60 – 90, конечно же, не являются эталоном идеальных женских пропорций для всех подряд. Пропорции тела вообще не могут быть одинаковыми для всех женщин, так как существуют различные типы телосложения, данные нам генетически.
Основные типы телосложения
К основным типам телосложения можно отнести астенический (тонкокостный), нормостенический (нормокостный) и гиперстенический (ширококостный).
- У женщин, имеющих астенический (тонкокостный) тип телосложения, тонкая кость, длинные конечности, тонкая шея, мышцы развиты сравнительно слабо. Представительницы этого типа обычно имеют небольшой вес, они энергичны и подвижны. Обильное питание довольно долго не приводит их к увеличению массы тела, так как они тратят энергию быстрее, чем накапливают. Если у женщины такого типа не очень тонкая талия и нормальные не узкие бедра все кажется миниатюрным из-за тонкой кости.
- Телосложение женщин нормостеников (нормокостньй тип) отличается пропорциональностью основных размеров тела, правильным соотношением. Самые красивые женские фигуры встречаются именно при таком типе телосложения.
- У представительниц гиперстенического (ширококостного) телосложения преобладают поперечные размеры тела. Их кости толстые и тяжелые, плечи, грудная клетка и бедра широкие, а ноги иногда несколько коротковаты. Женщинам такого типа, нужно помнить, что они склонны к полноте.
Определить примерный тип телосложения можно, измерив, окружность запястья рабочей руки. У нормостеников она равна 16-18,5 см, у астеников — 16 см, а у гиперстеников — 18,5 см.
Довольно часто встречаются смешанные виды телосложения с преобладанием параметров вышеуказанных типов.
Если говорить о градациях женского роста, то они следующие: низкий рост — 150 см и ниже, ниже среднего роста — 151-156 см, средний рост — 157-167 см, высокий — 168-175 см, очень высокий — 176 см и выше.
Правда в последние годы такая градация нуждаются в изменении с учетом акселерации современной молодежи, поэтому нормальным ростом можно считать для нормокостных и ширококостных от 166 до 170 см, а для тонкокостных от 168 до 172 см.
Правильные ноги
Между ростом и длиной ног существуют определенные пропорции.
Короткими можно считать ноги, если их длина меньше половины роста. Пропорциональной можно считать фигуру, когда длина ног больше половины роста. Для ширококостных желательно на 2-4 см, для нормокостных на 4-6 см, для тонкокостных на 6-9 см. Например, если при нормокостном типе телосложения с ростом 168 см длина ног равна 90 см, то это идеально.
Длину ног нужно измерять от выступа бедренной кости, до пола. В тех случаях, когда ноги несколько короче принятой нормы, изменить это соотношение поможет обувь на каблуке, так как зрительно она устраняет имеющуюся диспропорцию.
Диаметр же ноги в икре в зависимости от телосложения колеблется от 36 до 40 сантиметров, в щиколотке от 16 до 20 см. Специалисты даже пробовали составить таблицу идеальной формы ног в зависимости от типа телосложения.
Вот примерные параметры: при росте 156 и весе 50 – 55 кг — окружность ноги у бедра от 48 до 54 см, в икре 31-32 см, в щиколотке 18-20 см; при росте 160 и весе 55–58 кг — окружность ноги у бедра – от 50 до 56 см, в икре 32 – 35 см, в щиколотке 19 – 22 см; при росте 167 и весе 56-65 кг окружность ноги у бедра от 52 до 58 см, в икре 33- 36 см, в щиколотке 22 -23 см.
И кроме всего идеальные ноги должны иметь между собой три просвета. Для этого нужно встать перед большим зеркалом и поставить ноги в позицию – пятки вместе, носки врозь. Вы должны увидеть первый просвет под коленками, второй в области лодыжек, третий в верхней части ближе к бедрам. В остальных местах ноги должны сходиться.
Правильный вес
Масса тела зависит от типа телосложения, роста и, что очень важно, возраста человека. Один из вариантов расчета вес — это индекс Кетле. Согласно этому индексу, женщинам, имеющим тонкокостный тип телосложения, достаточно иметь 325 г на каждый сантиметр роста, для нормокостных — 350 и для ширококостных — 375 г. Затем индекс умножается на рост, и получается соответствующий вашим параметрам вес.
Необходимо подчеркнуть, что идеальный вес женщин, особенно тех, чей рост ниже 160 см, должен быть меньше нормального на 10-15%. Низкорослым женщинам, по меньшей мере до 20 лет, желательно иметь вес на 3-5 кг меньше нормального, т.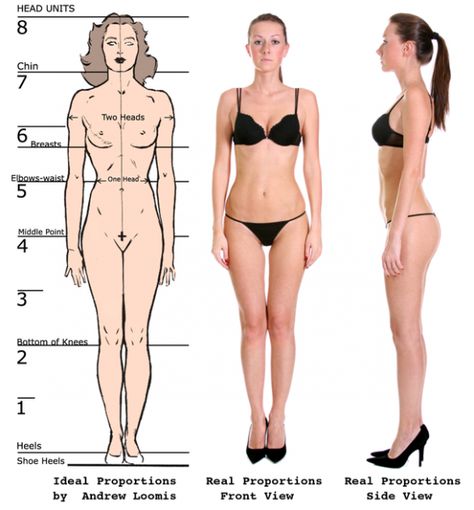
е. рассчитанного по индексу Кетле.
Как уже говорилось выше, масса тела зависит и от возраста. В таблице приведен коэффициент соотношения веса и роста (вес в г делится на рост в см) для женщин возраста от 15 до 40 лет.
|
|
| ||
|
|
|
| |
|
|
|
|
|
Чтобы определить свой нормальный вес, надо умножить рост в см на весо-ростовой коэффициент, соответствующий вашему возрасту и типу телосложения.
Излишки веса можно отследить измерив жировую складку на брюшной стенке, выше пупка, в 3 см от средней линии. Ее толщина в норме должна быть от 1 до 2 см.
Бедра, талия и грудь
Знание окружностей тела — груди, талии и бедер также помогает определить правильность телосложения. Такой показатель называется «вайтлз».
Нормальными показателями вайтлза для молодых женщин (18 – 28 лет) нормостенического типа телосложения можно считать, если окружность грудной клетки ровна половине роста плюс 2-5 см, для бюста — окружность грудной клетки плюс 8-10 см, для талии — рост стоя, минус 100, бедра должны быть больше окружности талии примерно на 25 -30 см. Для тонкокостных женщин можно считать нормой, если окружность их грудной клетки находится в пределах 84-86 см, а бюста — плюс 4-6 см к указанным цифрам.
Талия, обычно, у них тонкая, и находится в пределах 60-64 см, а окружность бедер больше, примерно, на 25 — 30 см.
У женщин, имеющих ширококостный тип телосложения, окружность грудной клетки превышает половину роста на 8-10 см, груди — еще на 8-10 см. Окружность талии при росте 166-168 см находится в пределах 70-76 см, а окружность бедер больше на те же 25-30 см.
Примерно к такому же выводу вначале девяностых годов пришел профессор психологии университета штата Техас Девендра Сингх. Только он исчислял пропорцию между бедрами и талией в процентном соотношении Согласно его теории, идеальными считаются пропорции, при которых объем талии, составляет от 60 до70% от объема бедер.
Для этого нужно объем талии разделить на объем бедер, полученный коэффициент должен быть от 0.6 до 0.7. Кстати, идеальными красавицами по этому соотношению являются Венера Милосская — 70% и Обнаженная Рубенса, те же 70%. А вот среди реальных женщин идеальны в соотношении талия – бедра: Мэрилин Монро 0,61 (56/91,5), Брижит Бардо 0,66 (58,5/89), Деми Мур 0,72 (66/91), Клаудиа Шиффер 0,67 (62/92), Синди Кроуфорд 0,69 (58/84), Жизель Бундхен 0.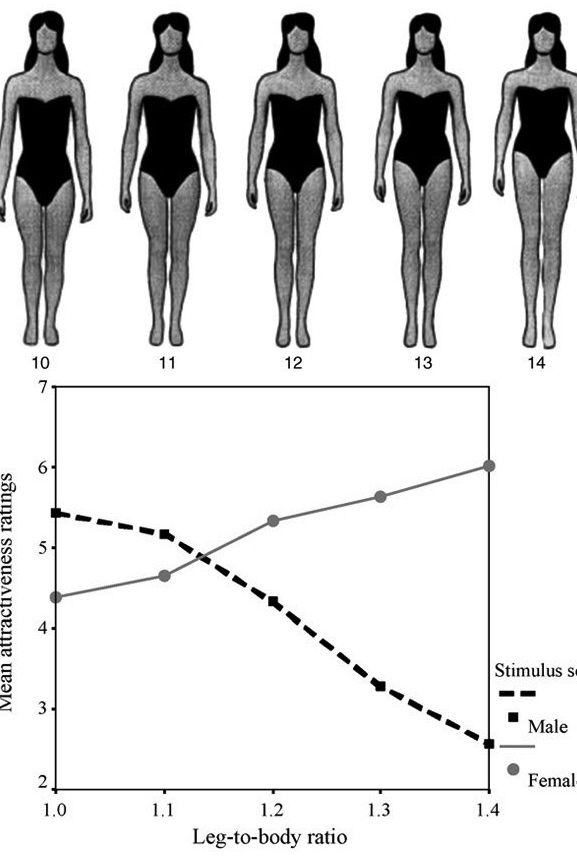
70 (61/86), Кайли Миноуг 0.70 (63/89).
Врачи же считают, что соотношение окружности талии к окружности бедер не должно превышать коэффициента эндокринного равновесия, который равен 0,85. Если ваша талия не превышает 85% от объема бедер, значит ваша фигура в полном порядке и с эстетической, и с медицинской точки зрения.
Время движется вперед, появляются новые критерии оценки красоты женской фигуры. Последний анализ результатов антропометрического обследования женщин, проводившийся в нашей стране в начале 2000 годов показал существенные изменения пропорций тела. У молодых женщин стали более длинные руки, ноги, более высокий уровень линии талии, более широкие плечи при той же величине туловища, улучшилась осанка. Так что можно сделать вывод, что молодое и среднее поколения женщин стало выше и стройнее, чем поколение предыдущее. Ну а если ваши параметры не совпадают с идеальными, не огорчайтесь! Все-таки самое главное в женщине ее индивидуальность ну и, конечно, ухоженный вид.
7 Рисунок Рисунок Пропорции, которые нужно знать
- Главная
- Рисунок Рисунок
- Пропорции рисунка
На протяжении веков художники были очарованы задачей изображения точных пропорций человеческого тела.
Было предпринято бесчисленное множество попыток стандартизировать пропорции рисунка фигуры и установить пропорциональные правила, которым необходимо следовать при изображении тела.
Однако, наблюдая, сколько существует систем измерения пропорций (или «каноны» как их называют) должны быть нашим первым признаком того, насколько открыты для интерпретации пропорции и что, возможно, ни одна пропорциональная система не может быть неизменно точной.
Что такое пропорции?
Пропорции
отношения или отношения 90 021 между высотой, шириной и глубиной предмета.
Чтобы нарисовать правдоподобное изображение какого-либо предмета, не
независимо от того, что или кто это, мы должны нарисовать пропорциональные отношения, как они проявляются на этом конкретном
предмет.
Например, на рисунке справа высота и ширина отверстия кружки примерно равны, а глубина составляет около полутора ширины. Эти
пропорции характерны для этого кружка в это конкретный сценарий.
Что бы
произойдет, если я изменил эти пропорции? Нарисованная кружка не совсем походила бы на
рожу, которую я наблюдал, но она все равно могла выглядеть правдоподобно и убедительно.
В случае фигуры или портрета, однако, случайно
изменение пропорций может создать очень заметные искажения, которые уменьшат правдоподобность вашего рисунка. Незначительные неточности в рисунке
пропорции рисунка уменьшают подобие вашего рисунка, в то время как основные
неточности могут нарушить логику тела и заставить его выглядеть
анатомически неточно.
Неудивительно, что художники на протяжении веков пытались
стандартизируйте эти измерения! Конечно, было бы удобно иметь возможность
полагаться на заученную пропорциональную систему… но можем ли мы действительно полагаться на одну из этих систем независимо от того, кого мы рисуем? Чтобы ответить на этот вопрос, давайте
посмотрите краткую историю пропорциональных канонов.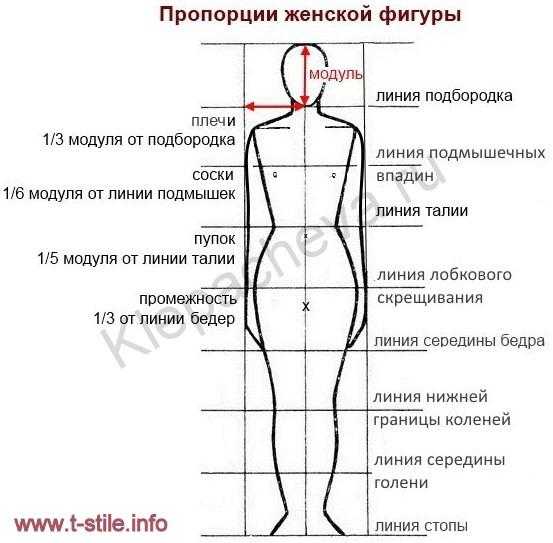
Краткая история
Пропорциональные каноны
Каждый канон (система измерения пропорций) — это поиск определенного идеала красоты. Однако, поскольку представление о красоте столь субъективно, подвижно и постоянно меняется, такими же были и каноны на протяжении всей истории.
Например, знаменитый греческий канон, созданный Поликлитом, описывает сильного атлета мужского пола, преуспевшего в гимнастике и обращении с оружием.
Типичным примером этого канона является Дорифор, одна из самых известных скульптур классической эпохи.
Однако так же, как сегодня мало тел, которые соответствуют современным представлениям об «идеальном» теле, вполне вероятно, что немногие тела во времена Поликлета соответствовали «идеальному» типу тела дорифора.
Римская копия Дорифора
Еще одной целью канонов является создание единицы
измерения, чтобы разделить тело на более управляемые, измеримые
участки, которые бы установили эти «идеальные» пропорции.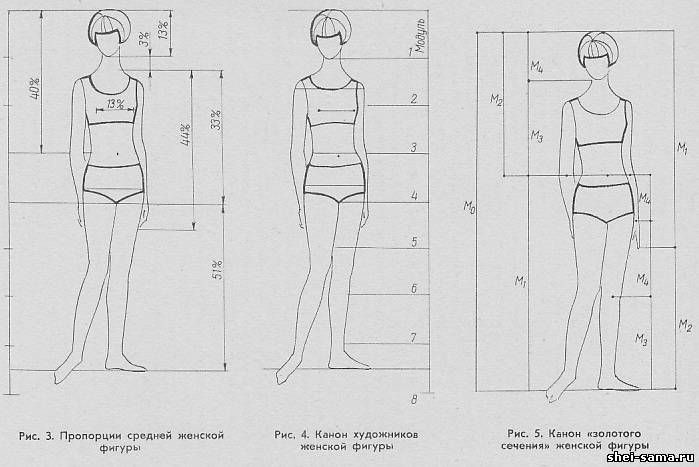
Например, в
самый старый известный текст о пропорциях, который был египетским каноном, длина
В качестве единицы измерения был выбран средний палец. Считалось, что он равен
до одной девятнадцатой части общей высоты тела.
В греческом каноне Поликлета в качестве единицы измерения выбрана ладонь руки.
Марк Витрувий, римский архитектор и писатель первого века до нашей эры, считал, что высота фигуры составляет восемь голов или десять лиц.
Леонардо да Винчи продемонстрировал многие идеи Витрувия о пропорциях в известном изображении человека в двух наложенных друг на друга позициях, вписанных в квадрат и круг: «Витрувианский человек».
Пропорциональные каноны
современности
Как вы уже догадались, поиск идеального измерения
система довольно бессмысленна. Существует так много различий в телах среди людей, что невозможно для всех вписаться в какой-либо набор стандартов.
уникальные качества каждого человека являются частью проблемы, сложности и
увлечение изображением фигуры.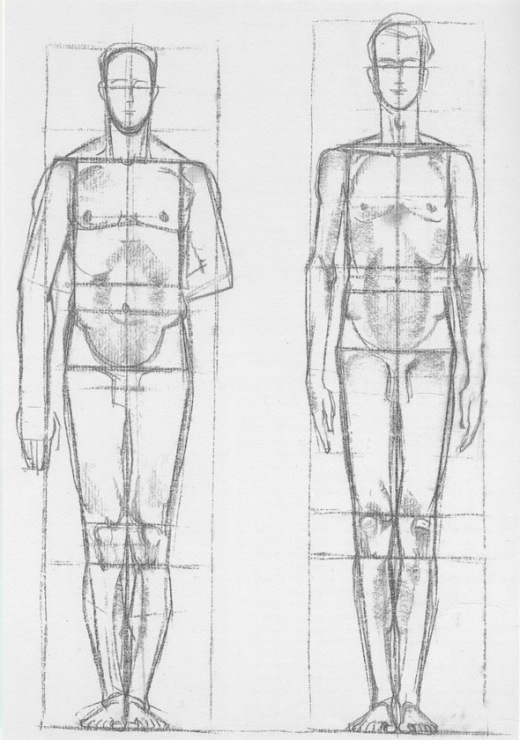
Однако:
Знание некоторых общих пропорций может быть полезным для наших рисунков, если мы
используем эти знания в сочетании с чутким наблюдением за моделью.
На сегодняшний день наиболее распространенной единицей измерения является голова
фигура, и обычно считается, что эта фигура имеет рост от 7,5 до 8 голов. (Голова также является отличным местом для начала рисования фигуры, о чем вы можете прочитать в статье 5 способов начать рисование фигуры .)
Какая разница между 7,5 и 8 головами?
Фигура высотой 8 голов будет значительно длиннее
ноги, например, у модели с подиума или героической фигурки. Более реалистичный
фигура примерно 7,5 головы в высоту, хотя, как я буду продолжать указывать
на протяжении всей этой статьи это обобщения, и их не следует принимать в качестве правил.
7 Пропорции рисования фигуры, которые нужно знать
Прежде чем углубляться в пропорции рисования фигуры, которые я считаю наиболее полезными
чтобы помнить, обратите внимание, что эти пропорции относятся к стоящей фигуре.
Когда фигура наклоняется к вам или от вас, садится или ложится, измерения становятся более сложными и иногда нечеткими, и часто больше не попадают в пропорции, перечисленные ниже.
БЕСПЛАТНАЯ ЗАГРУЗКА
В конце этой статьи вы получите бесплатную инфографику Пропорции рисунка, которые нужно знать , чтобы использовать ее в качестве напоминания об этих основных пропорциях!
В положении стоя следует помнить о следующих пропорциях рисунка семи фигур:
1. Высота фигуры примерно 7,5 головы.
2. Примерно на две головы вниз от верха рисунка проходит линия сосков.
3. Примерно в трех головах вниз от верхней части фигуры находится пупок, или пупок.
4. Примерно на четыре головы вниз от верхней части рисунка находится лобковая кость.
5. Лобковая кость находится примерно посередине тела.
6.
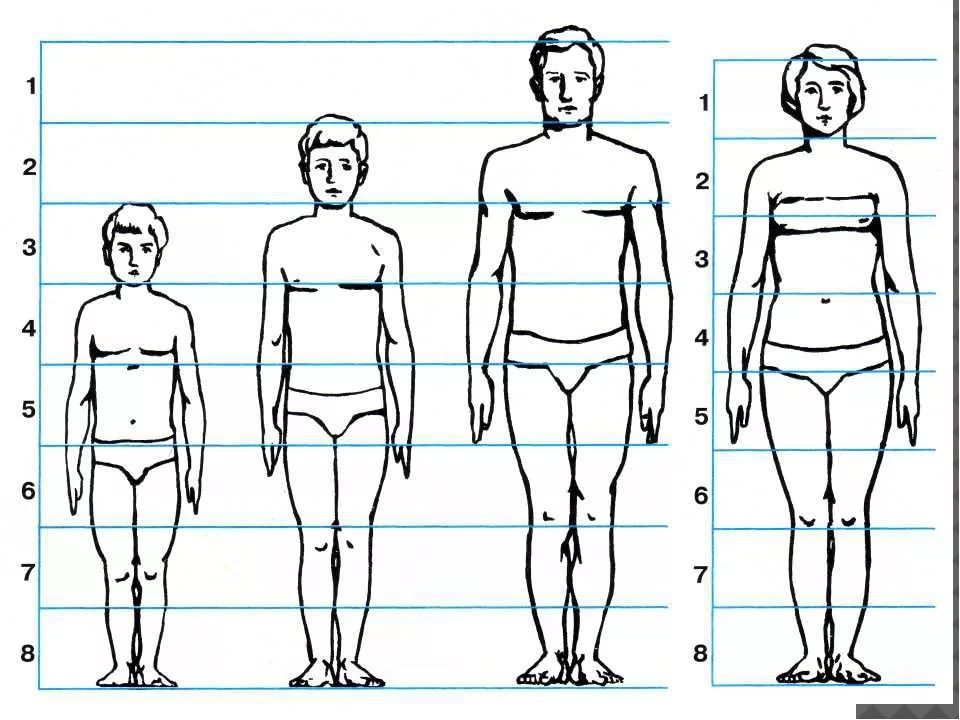Запястья выровнены с большими вертелами бедренных костей (верхняя кость голени).
7. Локти на одной линии с пупком.
Плюсы
и Минусы
использования пропорциональных систем:
Минусы:
- сильно полагаясь на заученные пропорции, вы можете
стать ленивым в наблюдении за моделью, что может привести к общим чертежам - , потому что существует так много различий в типах телосложения, нет
Пропорциональная система может быть принята как «правило»
Плюсы:
- пропорциональная система дает вам общее справочное руководство для оценки относительной длины и ширины тела
- пропорции могут привести к более точным и убедительным рисункам, если их использовать для сравнения с пропорциями на модели Например, аниматор может намеренно удлинить фигуру до 8 или 8,5 головы, если он намерен нарисовать героическую фигуру
Эффективное использование пропорций рисунка
Интересно, что пропорциональные системы могут привести к тому, что ваши рисунки
быть более общим или более конкретным, в зависимости от того, как вы их используете.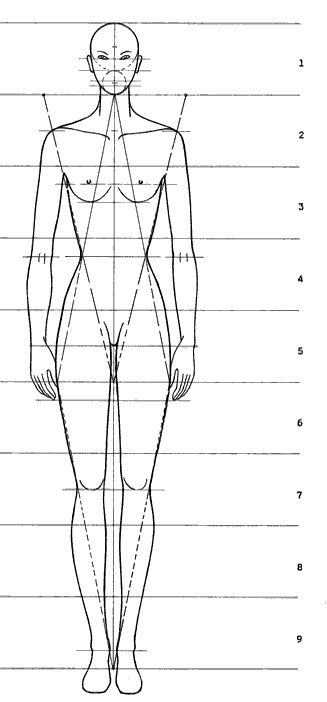
Как мы
достичь большей конкретности и точности с нашими знаниями о пропорциях?
Вместо того, чтобы предполагать, что модель будет иметь точную
пропорции, указанные выше, используйте их для проверки вариаций на рисунке.
Например, если вы знаете, что пупок обычно находится на три головы ниже
верхняя часть рисунка, измерьте и проверьте
чтобы увидеть, верно ли это для вашей модели (как я делаю в этом пошаговом руководстве по рисованию фигур).
Если это не так, в процессе измерения вы будете
способен определить, насколько выше или ниже должен быть пупок, чем три головы вниз
точку и нарисуйте ее там, где она появляется на конкретном человеке, которым вы являетесь.
наблюдая.
Это повышенная чувствительность, о которой вы знаете.
пропорции могут привести к вашему наблюдению, что будет иметь значение в
ваши рисунки, в большей степени, чем использование заученных пропорций рисунка фигуры.
Надеюсь, вам понравилась эта страница о пропорциях рисования фигур! Что дальше? Загрузите инфографику пропорций рисунка фигуры ниже и прокрутите вниз, чтобы просмотреть соответствующие страницы, которые могут вас заинтересовать.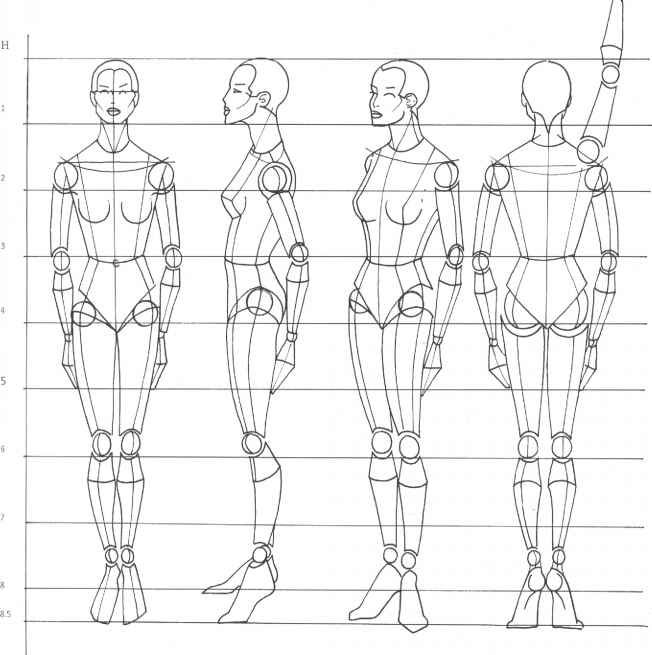
Приятного рисования!
БЕСПЛАТНАЯ ЗАГРУЗКА
Загрузите бесплатную инфографику Figure Drawing Proportions Infographic
Drawing Resource Library — только для участников!
Если вам понравилась эта страница о пропорциях рисования фигур, вас также могут заинтересовать …
Родственные страницы
5 способов начать рисовать фигуру
Пошаговое руководство по рисованию фигуры
7 исследований для улучшения рисования фигуры
5 пропорций лица, которые нужно знать знать
Вернуться на домашнюю страницу из 7 Пропорции рисования рисунков знать
Пропорции и подобные фигуры — объяснение!
СоотношенияПропорцииПропорциональностьРешение словесных задачЛучи солнца / Части
Purplemath
Уравнения пропорциональности можно использовать для «решения» «подобных фигур».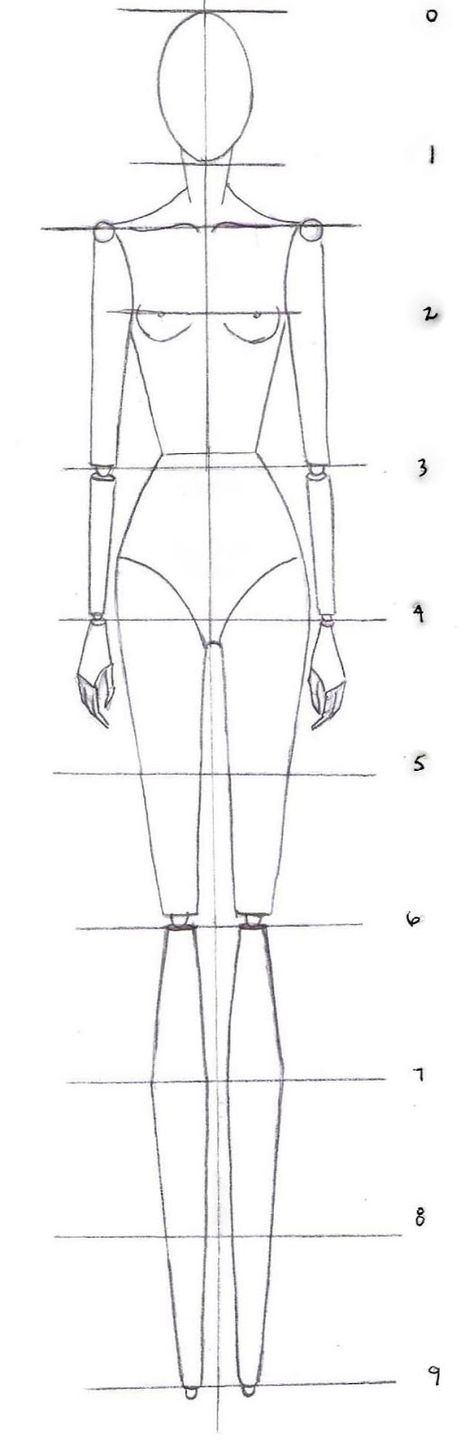
Что такое «похожие фигуры»?
«Подобный» — это геометрический термин, относящийся к геометрическим фигурам (квадратам, треугольникам и т. д.), которые имеют одинаковую форму, но одна из пар фигур больше другой.
Содержание продолжается ниже
MathHelp.com
Решение пропорций
Чтобы мысленно представить похожие фигуры, подумайте о том, что происходит, когда вы используете настройку «увеличить» или «уменьшить» на копировальном аппарате или когда вы получаете восьмерку. увеличение изображения размером три на пять раз, которое вам действительно нравится, или, если вы использовали графическую программу, подумайте о сохранении «соотношения сторон» изображения, размер которого вы изменяете. Результатом каждого из этих примеров является пара похожих фигур (или, во всяком случае, похожих картинок).
Как вы «решаете» подобные фигуры?
В контексте соотношений и пропорций точка подобия заключается в том, что соответствующие стороны подобных фигур пропорциональны; то есть длины совпадающих сторон пропорциональны.
Таким образом, имея две похожие фигуры, не все стороны которых отмечены их длинами, вы можете создать уравнение пропорциональности, смешивая известную и неизвестную информацию, и найти неизвестное значение.
Примечание. Чтобы этот процесс работал, у подобных фигур должна быть хотя бы одна пара соответствующих сторон, обе длины которых известны. Эта пара будет вашей эталонной парой, формируя одну сторону вашего уравнения пропорциональности.
Например, посмотрите на подобные треугольники ABC и abc ниже:
«Соответствующие стороны» — это пары сторон, которые «совпадают», за исключением аспекта увеличения или уменьшения их относительных размеров. Таким образом, А соответствует а, В соответствует b, а С соответствует с.
Так как эти треугольники подобны, то пары соответствующих сторон пропорциональны. То есть A : a = B : b = C : c. Другими словами, это уравнение, состоящее из трех частей, гласит: «Большой-А относится к маленькому-А, как большой-В к маленькому-В и как большой-С к маленькому-С».
Эта пропорциональность соответствующих сторон может быть использована для нахождения длины стороны фигуры, учитывая аналогичную фигуру, для которой известны достаточные измерения.
- В показанных треугольниках длины сторон даны как A = 48 мм, B = 81 мм, C = 68 мм и a = 21 мм. Найдите длины сторон b и c, округлив до ближайшего целого числа.
Я составлю свои пропорции, используя соотношения в форме (длина большого треугольника) ÷ (длина маленького треугольника), а затем решу пропорции. (Кстати, вы можете установить свои пропорции по своему усмотрению; нет правила, которое гласит, что «чем больше, тем выше».)
Так как они дали мне только длину стороны a для маленького треугольника, мое эталонное соотношение будет A : a.
Сначала я найду длину b. Вот моя установка:
(Нет необходимости маркировать вещи, как я сделал выше, с начальной дробью, содержащей слова «большой» и «маленький», но это может быть очень полезно, чтобы напомнить себе, как вы Я хочу все наладить.
Это быстрый способ уберечь себя от неприятностей.)
Заполнив мои известные значения, я получаю:
б = [21 × 81]/48
б = 1701/48
b = 35,4375
(мне нужно будет не забыть дать округленное до целого значение длины этой стороны (другими словами, мне нужно будет не забыть округлить до «35») в моей руке -в ответ.)
Теперь, когда я нашел одну длину, я тем же методом найду длину оставшейся стороны, c.
с × 48 = 21 × 68
с = 1428/48
c = 29,75
В качестве ответа я мог бы просто записать два числа, которые я нашел, но эти числа не будут иметь большого смысла без их единиц измерения. Кроме того, при повторной проверке исходного упражнения мне напомнили, что я должен округлить свои значения до ближайшего целого числа, поэтому «29,75» с единицами измерения или без них будет неправильным.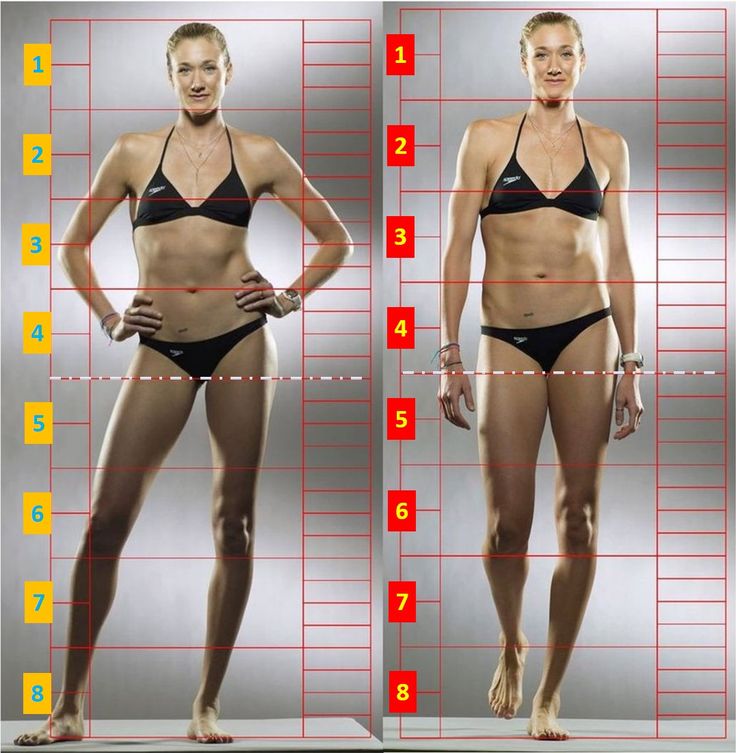
Правильный ответ:
b = 35 мм, c = 30 мм
Хотя я мог бы использовать длину, найденную для b, для нахождения длины c в приведенном выше упражнении, вместо этого я вернулся к значению а. Почему? Потому что это было заведомо хорошее «точное» значение.
Хотя десятичное значение в этом случае было точным значением (то есть значение b не округлялось), обычно лучше иметь привычку возвращаться к заведомо правильным значениям, когда это возможно. Таким образом, когда десятичное значение округлено до , вы игнорируете округленное производное значение и возвращаетесь к точному исходному значению.
Эта практика поможет вам избежать потенциальных ошибок округления.
- Картинка размером 3,5″ (то есть 3,5 дюйма) в высоту и 5″ в ширину должна быть увеличена до ширины 9″. Какой высоты будет картина?
Фотолаборатория при увеличении исходного изображения будет сохранять пропорции оригинала; то есть прямоугольники, представляющие внешние края исходного и увеличенного изображения, будут похожими фигурами.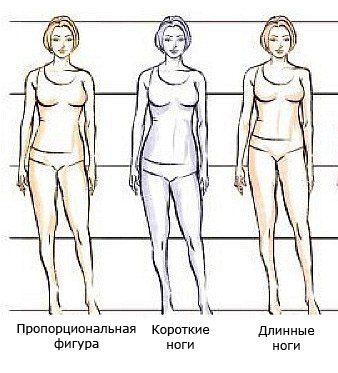
Используя этот факт, я могу установить пропорцию и решить, используя « h » для обозначения значения высоты, которое я ищу:
h = [(9)(3,5)]/5
31,5 = 5 ч = 31,5/5
h = 6,3
Высота изображения будет:
6,3 дюйма
В первом упражнении выше отношения были между соответствующими сторонами, и пропорциональность была сформирована из этих пар сторон. Соотношения в пропорциях содержали дроби, образованные от деления первоначального большого значения на новое малое значение. Во втором упражнении выше отношения были между двумя разными измерениями, а пропорциональность была сформирована из наборов измерений. Соотношения в пропорции содержат дроби, образованные от старой высоты и старой ширины, и от новой высоты и новой ширины.
Для многих упражнений вы сможете установить соотношение и пропорции несколькими способами.
Это совершенно нормально. Просто убедитесь, что вы хорошо маркируете вещи, четко определяете свои переменные и настраиваете их разумным и последовательным образом. Это должно помочь вам найти правильные решения. Если вы когда-либо сомневались в своем решении, не забудьте снова подключить его к исходному упражнению и убедиться, что оно работает.
Есть еще одна тема, своего рода ответвление однотипных вопросов, с которыми вы можете столкнуться. Он основан на том факте, что если две фигуры (или трехмерные фигуры) подобны, то пропорциональны не только их длины, но и их квадраты (будучи их площадями) и их кубы (будучи их объемами).
- Две прямоугольные призмы подобны, одна пара соответствующих длин составляет 15 см и 27 см соответственно. (а) Если объем меньшей призмы равен 2000 см 3 , каков объем большей призмы? (б) Если площадь одной грани большей призмы составляет 243 см 2 , какова площадь соответствующей стороны меньшей призмы?
«Прямоугольная призма» — это просто причудливая геометрическая фраза для «кирпича», поэтому я знаю, что работаю с трехмерными фигурами.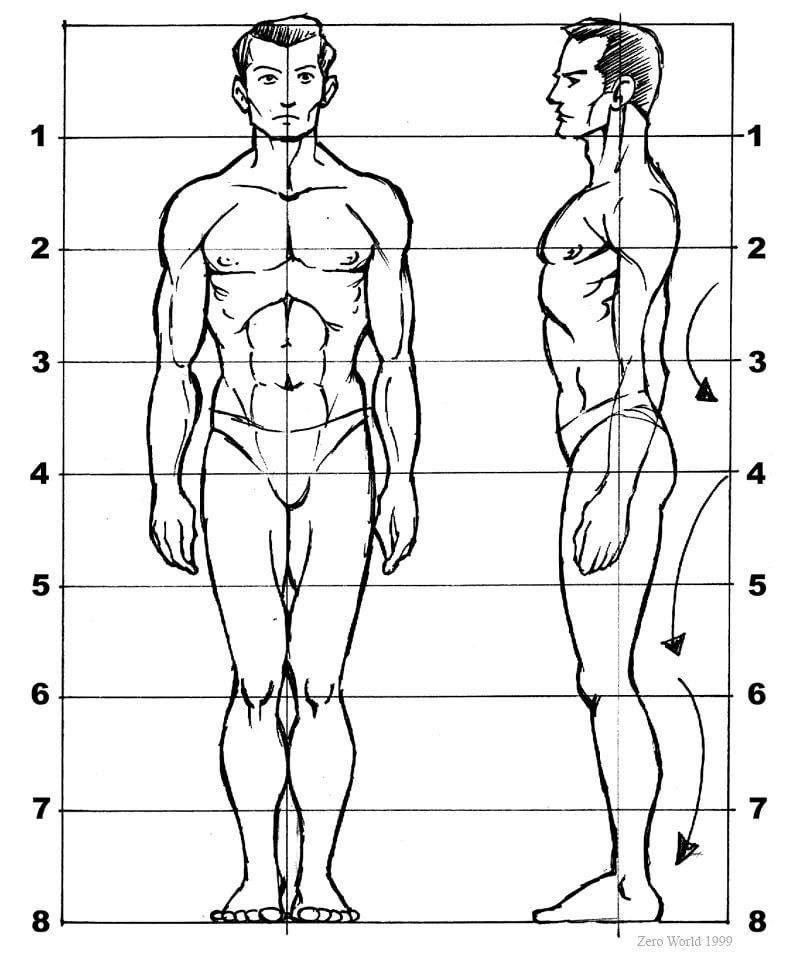
Мне известно, что формы похожи, и мне предоставлены две сравнительные длины. Это дает мне мое основное соотношение:
(маленький)/(большой): 15/27 = 5/9
Это
5/9 представляет собой упрощенное (т. буду использовать для нахождения моих ответов для объема и площади поверхности.
(a) Чтобы найти объем большей призмы, мне нужно возвести в куб линейное отношение, которое они мне дали (то есть мне нужно возвести в куб уменьшенную дробь, которую я получил, когда поместил две длины в отношение выше). Помещая значения для меньшей призмы в верхнюю часть коэффициентов, я получаю:
(5/9) 3 = 125/729
Вот соотношение, которое я буду использовать для настройки пропорции объема:
V 90905 = [(2000] /125
В = 11664
Проверив свои единицы измерения, я получил ответ:
(а) 11 664 см 3
(б) Чтобы найти площадь одной стороны меньшей призмы, мне нужно чтобы возвести в квадрат линейное отношение, которое они мне дали (то есть мне нужно возвести в квадрат уменьшенную дробь, полученную путем помещения двух длин в отношение).